佐藤の数学教科書「微分」編の勉強
なめらかな曲線の接線は、微分によって初めて正しく定義できる。
(接線を求める式に重根が含まれるとは限らない。)
【問1】2つの放物線
y= x2 (式1)
y=-(x-2)2 (式2)
の共通接線の方程式を求めよ。
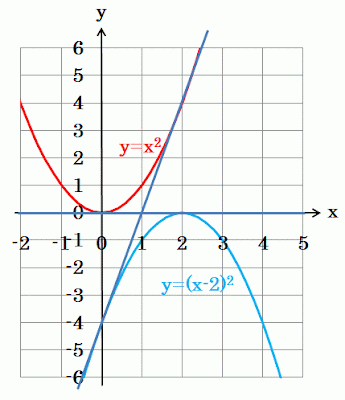
(解答の方針)
式1の接点A(a,b)での接線の式をあらわし、
式2の接点C(c,d)での接線の式をあらわし、
それらの接線の式が等しいとする方程式を書いて、
その方程式を解けば良い。
ただし、その方程式を解く過程で計算間違いをすると正しい答えが出ない。
そのため、計算間違いを少なくする問題の解き方を工夫する。
(解答)
y= x2 (式1)
y=-(x-2)2 (式2)
(1)
式1を微分して式1のグラフの傾きを求める。
y’=2x (式3)
接点A(a,a2)での式1の接線の式は
傾きy’=2a
だから、以下の式になる。
y-a2=y’(x-a)
y-a2=2a(x-a) (式4)
(2)
式2を微分して式2のグラフの傾きを求める。
y’=-2(x-2) (式5)
接点C(c,-(c-2)2)での式2の接線の式は
傾きy’=-2(c-2)
だから、以下の式になる。
y+(c-2)2=y’(x-c)
y+(c-2)2=-2(c-2)(x-c)
この式を、
c-2=e (式6)
とおいて、以下のように単純な式であらわす。
y+e2=-2e(x-c) (式7)
このように単純な形に式をあらわすことで、計算が簡単になり、計算間違いを少なくすることができる。
式7に残っているcもeにおきかえる。
y+e2=-2e(x-e-2) (式8)
(3)
接線の式8と4の傾きが等しい条件式を求める。
-2e=2a
e=-a (式9)
(4)
式4と式8のそれ以外の項も等しくなる条件式を求める。
e2+2e(-e-2)=-a2+2a・a
-e2-4e=a2
式9を代入してeをaにおきかえる。
-a2+4a=a2
-2a2+4a=0
a(a-2)=0
a=0 (式10)
or
a=2 (式11)
(5)式10の場合:
a=0 (式10)
式10を式4に代入。
y=0 (式12)
(6)式11の場合:
a=2 (式11)
式11を式4に代入。
y-4=4(x-2)
y=4x-4 (式13)
以上の結果、式1と2の放物線の共通接線の方程式は、
y=0 (式12)
と、
y=4x-4 (式13)
である。
(解答おわり)
リンク:
高校数学の目次