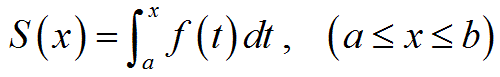「微分・積分」の勉強
高校の数Ⅱで、微分・積分を学ぶようになり、その勉強がつまらなくなり数学を学ぶのをあきらめて文系に進むことにする学生が多いらしい。そうなる以前に早めに数学がつまらなくなることを見切って早々と文系に進むことに決める学生も多いらしい。
そのため、このページでは、「微分・積分」をどうすればおもしろく勉強できるかというコツを考えます。
（当ブログの結論）
高校２年生が微分積分を学習するのに適切な本は、高校生用の教科書や参考書なのでは無く、大学１年生向けの参考書：例えば：
「やさしく学べる微分積分」（石村園子）
書評「素晴らしいほどわかりやすい。 高校2年の知識があれば、すらすら読める。 数学苦手な人でも、やさしくシリーズは、微積とベクトルはとっつきやすいと思うので、おすすめです。」
などだと思います。
その本は、初めて微分積分を学ぶ高校２年生にとって、内容がわかり易いです。説明が正確でごまかしが無いので、高校教科書の微分積分の説明にあるようなごまかしが納得できず（ごまかしに納得する方がおかしい）学習が止まってしまう様なことが無く、スムーズに勉強を進めることできるので良いと思います。その本の３６ページから４５ページまで勉強するだけで、微分の必須知識が学べます。
当ブログでは、先ず、勉強の順番が、
（１）極限
（２）微分
（３）積分
になっている事が、
「微分・積分」の勉強をつまらなくしていると考えます。
数学が好きでいつも数学を勉強している学生は、「微分・積分」の授業の順番には「微分・積分」を学んでいないと考えます。
数学の問題を多く解いていて、数学の問題を解く技術を磨いてきた学生は、「微分・積分」の基礎的な概念は既に考えたことがあり、その概念も利用して問題を解いている。
そして、「微分・積分」の授業に出会ったら、既に知っている自分の知識を整理するために役立てようとして授業を聞くから、「微分・積分」の勉強ができるのだと考えます。
その、既に知っている「微分・積分」の知識とは、どのようなものかを以下で考えます。
数学が好きでいつも数学を勉強している学生は、好奇心を満足させる面白いテーマの順に数学を学んで行くと思います。
面白い数学の課題を見つける都度、その課題を自分で研究するという道草を食います。その道草の１つに、基礎的な「微分・積分」の概念の修得があると思います。
そのため、以下では、その、面白い順に、微分積分を学んでいこうと思います。
（１）積分
（２）微分
（３）極限
の概念の順に学ぶのが面白く、
それを学んだら、
（４）極限の概念の精密化
（５）微分の知識の整理
（６）積分の知識の整理
を勉強するのが、勉強の順番として適切だと考えます。
（１）積分：
以下の問題を考えます。
【問題１】
なぜ、三角錐の体積Ｖは、
体積Ｖ＝底面積Ｓ×高さｈ×（１／３）
なのか。
この公式は、何とか覚えられたと思いますが、
もっと、すっきり覚える方法が無いか？
と考えたことがあると思います。
この問題は、以下の様に分析することができます。
この解に法則性があるように思われますが、
この問題は難しいので、これを解くための準備として、
この問題をもっとやさしくした以下の問題を先に解くことにします。
【問題２】
なぜ、三角形の面積Ｓは、Ｓ＝底辺Ｌ×高さｈ×（１／２）
なのか。
この問題ならば、上のような場合を考えて、解くためのヒントを見つけることができます。
この問題２で得られたヒントを拡張して、
以下の様に問題１を解析します。
【問題１（再）】
これは、以下のグラフの面積を分割して計算することに対応すると考えることができます。
（この計算で用いた２乗の数列の和の式はここをクリックした先のページにあります）
このように問題を解析することで、後は、この２次関数のグラフの面積を与える法則性を把握すれば、この種の問題が自由に解けるようになることが理解できます。
この様に、分割した要素の総計を求めてグラフの面積を計算する手法が「積分」です。
また、その計算のための法則性を整理して覚えることが「積分」を勉強するということです。
もう１つ、分割した要素の総計を求める例を追加しておきます。
《グラフの微小増分の総和がグラフの高さになる》
上の図のように、グラフの傾きにΔｘを掛け算した要素は、グラフの高さの増分Δｙです。
上図のように、
グラフの高さの増分Δｙの総計＝グラフの高さｙ
になります。
（グラフの微小部分の総和おわり）
（応用例）
分割した要素の総和を考える応用例として、下図の点Ａまでの円弧の長さ θ と、長さｔａｎθ の点Ｔまでの垂直線の長さの大小関係を、
下図の平行線で分割した微小部分の大小関係から求めます。平行線で円弧θを切った部分の長さをΔθと表します。平行線で(1,0)の点から点Tまでの、長さがtanθの垂直な線分を切った部分の長さをΔ(tanθ)と表します。
円弧 θ を平行線で分割した微小ベクトルの平行線への射影成分Ｐθ の長さよりも、垂直な線分ｔａｎθ を平行線で分割した微小ベクトルの平行線への射影成分Ｐｔ の長さの方が長い。そのため、円弧θを平行線で分割した微小ベクトルの長さΔθよりも、垂直な線分tanθを平行線で分割した微小ベクトルの長さΔ(tanθ)の方が長い。
その個々の微小ベクトルの長さの総和（積分）を考えることで、
θ ＜ｔａｎθ という大小関係が分かりました。
（応用例おわり）
（積分の特徴）
積分とは、連続した階段を登ることに似ています。
先ず、階段の１歩１歩の段差は有限でなければならない。
無限の段差の階段は登れないので、それは積分できない。
積分は有限の階段でつながっている。
ある点からある点まで積分できたならば、必ず、その点間をつなぐ道が、どこかを通って、通じている。その点をつなぐ道は目前の無限の高さの崖では無いが、他の道が必ずあるのです。
（微分積分学の歴史）
ライプニッツが、1684年に「極大と極小にかんする新しい方法」を出版して、その中で微分法を発表し、
ついで1686年に「深遠な幾何学」を出版して積分法を発表しました。
その後に、ニュートンが微分積分学を発表しました。
それに対して、旧い数学者のバークレー司教(Bishop George Berkeley)が微分積分学を攻撃した論争が微分積分学を正しく育てました。
バークレー司教は、ダブリンのトリニティ・カレッジで神学を学び、後に講義をする。アイルランド、クロインの(英国国教会の)監督Bishopとなる(1734)。
バークレー司教は、数学から唯物論を追放する目的で、『解析者―不誠実な数学者へ向けての論説』（The Analyst: or a Discourse Addressed to an Infidel Mathematician, 1734）で、ニュートン・ライプニッツ理論（微分積分学）を攻撃し、大論争を引き起こす(『解析教程』第II章第1節参照)。
ド・モアブル、テイラー、マクローリン、ラグランジュ、ヤコブ・ベルヌーイ、ヨハン・ベルヌーイなどが論争に加わり、微積分学の論理的基礎づけに対する関心を高めた功績は大きい。
とくに、マクローリンは反論のためにニュートンの方法の厳密な構成を行った。
以下で、バークレー司教の微分積分学に対する感想を見てみます。
『バークレー司教：解析者より』
「しかし、速度の速度、その速度、そのまた速度、またその速度、またまたその速度などなどというのは、私が間違っているのでなければ、すべての人間の理解を越えてしまっています。
精神がこの捉え難いアイデア（微分積分学）を解析し追及すればするほど、それはまごつき狼狽えることになり.....」
『バークレー司教：解析者より』
「......我が時代の解析者（微分積分学）は有限の量の差を考えるだけでは満足しません。
彼ら（微分積分学）はさらにその差の差を考え、最初の差の差の差を考えます。 そしてさらに無限にまで。
つまり彼ら（微分積分学）は認識できる最小の量よりさらに無限に小さい量を考えます。
その無限に小さい量よりもさらに無限に小さな量を、そしてその上これまでの無限小量よりもさらに無限に小さい量を考え、終わりも限界もないのです。
......もう告白するしかありませんが、無限に小さい量を心に描くことは ......私の能力を超えています。
しかし、そのような無限に小さい量の、それよりさらに無限に小さい一部、だから結局それを無限倍したとしても最も微細な有限の量にまでなることもできない、そんなものを想像するということは、どんな人にとってもそれこそ無限に困難なことだろうと、私は思うのです。.....」
『バークレー司教：解析者より』
「そして、この流率（微分）とは何だろうか？
無限小の増分の速度。 そして、これら同じ無限小の増分の速度とは何なんだろうか？
これらは有限の量でもなく、無限に小さい量でもなく、無でもない。 こんなものなら、過ぎ去った量の幽霊と呼んではいけないというのだろうか？ 」
ニュートンとライプニッツの微分は、「無限小」の概念が十分に論理付けされていなかったため、今日のような厳密さが欠けていた。だが、微分は、力学や天文学などで応用可能、しかも実用的であったため、ベルヌーイやロピタル、オイラー、ラグランジュ、ラプラスなどの研究によって普及していった。
微分学が厳密性を伴うようになったのは、19世紀に入ってからである。仏の数学者コーシーは、1821年に発表した「解析教程」で「極限」や「無限小」、「連続関数」の概念を定義し、解析学の基礎を刷新し、その後デデキントやカントールによる実数論などを経て、今日の微分の基礎が完成した。
しかし、この、微分積分が歴史的に持っていたあいまいさとごまかしは、現在の日本の高校の微分積分の教育においては、更にごまかしが拡大されて教えられています。例えば、微分積分学の命綱が「連続関数」の概念ですが、高校数学では間違った定義が教えられています。以下で、その高校教育の実態を見ていきましょう。
連続関数の定義は1817年にBolzanoが中間値の定理を証明する前提条件に連続関数の定義が必要であることを明確にしてから、その定義が定まった。その歴史的経緯から、中間値の定理を成り立たせない関数を連続関数と呼ぶ高校数学での連続関数の定義は偽物である。なお、高校数学で定義された連続関数という言葉が使い物にならないので、大学数学では、連続関数という言葉を使わずに「区間連続」という言葉で本来の意味の連続関数をあらわすことにしています。
【閉区間で連続な関数の最大値・最小値の定理】
閉区間（ ａ≦ｘ≦ｂ）で連続な関数ｆ（ｘ）は、
その区間内で有限の値の最大値と最小値を持つ。
（ここまでが定理）
この定理は、誤った連続関数の定義と異なる、正しい連続関数の定義を前提にした定理です。そのため、この定理は、高校数学では無視することが強いられています。
高校数学では、
ｙ＝１／ｘは、ｘ＝０以外の、全ての定義域の点で連続なので「連続関数」と呼ばれています。
また、高校数学では、閉区間（ ａ≦ｘ≦ｂ）とは、変数ｘの値の範囲を限定する式のことであるという間違いが教えられています。
その誤った知識に基づくと、
【閉区間で連続な関数の最大値・最小値の定理】とは、
変数ｘの範囲（ ａ≦ｘ≦ｂ）内に関数が連続である定義域を持つ連続関数ｆ（ｘ）は、
その範囲（ ａ≦ｘ≦ｂ）内で有限の値の最大値と最小値を持つ。
（ここまでが定理）
という定理と解釈されます。
この「定理」には以下の反例があります。
関数ｆ（ｘ）＝１／ｘは、
変数ｘの範囲
－１≦ｘ≦１
内に定義域（ただしｘ≠０という定義域）が存在し、
－１≦ｘ≦１
内で定義されているどの点でも連続なので、
高校の数Ⅱで、微分・積分を学ぶようになり、その勉強がつまらなくなり数学を学ぶのをあきらめて文系に進むことにする学生が多いらしい。そうなる以前に早めに数学がつまらなくなることを見切って早々と文系に進むことに決める学生も多いらしい。
そのため、このページでは、「微分・積分」をどうすればおもしろく勉強できるかというコツを考えます。
（当ブログの結論）
高校２年生が微分積分を学習するのに適切な本は、高校生用の教科書や参考書なのでは無く、大学１年生向けの参考書：例えば：
「やさしく学べる微分積分」（石村園子）
書評「素晴らしいほどわかりやすい。 高校2年の知識があれば、すらすら読める。 数学苦手な人でも、やさしくシリーズは、微積とベクトルはとっつきやすいと思うので、おすすめです。」
などだと思います。
その本は、初めて微分積分を学ぶ高校２年生にとって、内容がわかり易いです。説明が正確でごまかしが無いので、高校教科書の微分積分の説明にあるようなごまかしが納得できず（ごまかしに納得する方がおかしい）学習が止まってしまう様なことが無く、スムーズに勉強を進めることできるので良いと思います。その本の３６ページから４５ページまで勉強するだけで、微分の必須知識が学べます。
当ブログでは、先ず、勉強の順番が、
（１）極限
（２）微分
（３）積分
になっている事が、
「微分・積分」の勉強をつまらなくしていると考えます。
数学が好きでいつも数学を勉強している学生は、「微分・積分」の授業の順番には「微分・積分」を学んでいないと考えます。
数学の問題を多く解いていて、数学の問題を解く技術を磨いてきた学生は、「微分・積分」の基礎的な概念は既に考えたことがあり、その概念も利用して問題を解いている。
そして、「微分・積分」の授業に出会ったら、既に知っている自分の知識を整理するために役立てようとして授業を聞くから、「微分・積分」の勉強ができるのだと考えます。
その、既に知っている「微分・積分」の知識とは、どのようなものかを以下で考えます。
数学が好きでいつも数学を勉強している学生は、好奇心を満足させる面白いテーマの順に数学を学んで行くと思います。
面白い数学の課題を見つける都度、その課題を自分で研究するという道草を食います。その道草の１つに、基礎的な「微分・積分」の概念の修得があると思います。
そのため、以下では、その、面白い順に、微分積分を学んでいこうと思います。
（１）積分
（２）微分
（３）極限
の概念の順に学ぶのが面白く、
それを学んだら、
（４）極限の概念の精密化
（５）微分の知識の整理
（６）積分の知識の整理
を勉強するのが、勉強の順番として適切だと考えます。
（１）積分：
以下の問題を考えます。
【問題１】
なぜ、三角錐の体積Ｖは、
体積Ｖ＝底面積Ｓ×高さｈ×（１／３）
なのか。
この公式は、何とか覚えられたと思いますが、
もっと、すっきり覚える方法が無いか？
と考えたことがあると思います。
この問題は、以下の様に分析することができます。
この問題は難しいので、これを解くための準備として、
この問題をもっとやさしくした以下の問題を先に解くことにします。
【問題２】
なぜ、三角形の面積Ｓは、Ｓ＝底辺Ｌ×高さｈ×（１／２）
なのか。
この問題２で得られたヒントを拡張して、
以下の様に問題１を解析します。
【問題１（再）】
このように問題を解析することで、後は、この２次関数のグラフの面積を与える法則性を把握すれば、この種の問題が自由に解けるようになることが理解できます。
この様に、分割した要素の総計を求めてグラフの面積を計算する手法が「積分」です。
また、その計算のための法則性を整理して覚えることが「積分」を勉強するということです。
もう１つ、分割した要素の総計を求める例を追加しておきます。
《グラフの微小増分の総和がグラフの高さになる》
上図のように、
グラフの高さの増分Δｙの総計＝グラフの高さｙ
になります。
（グラフの微小部分の総和おわり）
（応用例）
分割した要素の総和を考える応用例として、下図の点Ａまでの円弧の長さ θ と、長さｔａｎθ の点Ｔまでの垂直線の長さの大小関係を、
下図の平行線で分割した微小部分の大小関係から求めます。平行線で円弧θを切った部分の長さをΔθと表します。平行線で(1,0)の点から点Tまでの、長さがtanθの垂直な線分を切った部分の長さをΔ(tanθ)と表します。
その個々の微小ベクトルの長さの総和（積分）を考えることで、
θ ＜ｔａｎθ という大小関係が分かりました。
（応用例おわり）
（積分の特徴）
積分とは、連続した階段を登ることに似ています。
先ず、階段の１歩１歩の段差は有限でなければならない。
無限の段差の階段は登れないので、それは積分できない。
積分は有限の階段でつながっている。
ある点からある点まで積分できたならば、必ず、その点間をつなぐ道が、どこかを通って、通じている。その点をつなぐ道は目前の無限の高さの崖では無いが、他の道が必ずあるのです。
（微分積分学の歴史）
ライプニッツが、1684年に「極大と極小にかんする新しい方法」を出版して、その中で微分法を発表し、
ついで1686年に「深遠な幾何学」を出版して積分法を発表しました。
その後に、ニュートンが微分積分学を発表しました。
それに対して、旧い数学者のバークレー司教(Bishop George Berkeley)が微分積分学を攻撃した論争が微分積分学を正しく育てました。
バークレー司教は、ダブリンのトリニティ・カレッジで神学を学び、後に講義をする。アイルランド、クロインの(英国国教会の)監督Bishopとなる(1734)。
バークレー司教は、数学から唯物論を追放する目的で、『解析者―不誠実な数学者へ向けての論説』（The Analyst: or a Discourse Addressed to an Infidel Mathematician, 1734）で、ニュートン・ライプニッツ理論（微分積分学）を攻撃し、大論争を引き起こす(『解析教程』第II章第1節参照)。
ド・モアブル、テイラー、マクローリン、ラグランジュ、ヤコブ・ベルヌーイ、ヨハン・ベルヌーイなどが論争に加わり、微積分学の論理的基礎づけに対する関心を高めた功績は大きい。
とくに、マクローリンは反論のためにニュートンの方法の厳密な構成を行った。
以下で、バークレー司教の微分積分学に対する感想を見てみます。
『バークレー司教：解析者より』
「しかし、速度の速度、その速度、そのまた速度、またその速度、またまたその速度などなどというのは、私が間違っているのでなければ、すべての人間の理解を越えてしまっています。
精神がこの捉え難いアイデア（微分積分学）を解析し追及すればするほど、それはまごつき狼狽えることになり.....」
『バークレー司教：解析者より』
「......我が時代の解析者（微分積分学）は有限の量の差を考えるだけでは満足しません。
彼ら（微分積分学）はさらにその差の差を考え、最初の差の差の差を考えます。 そしてさらに無限にまで。
つまり彼ら（微分積分学）は認識できる最小の量よりさらに無限に小さい量を考えます。
その無限に小さい量よりもさらに無限に小さな量を、そしてその上これまでの無限小量よりもさらに無限に小さい量を考え、終わりも限界もないのです。
......もう告白するしかありませんが、無限に小さい量を心に描くことは ......私の能力を超えています。
しかし、そのような無限に小さい量の、それよりさらに無限に小さい一部、だから結局それを無限倍したとしても最も微細な有限の量にまでなることもできない、そんなものを想像するということは、どんな人にとってもそれこそ無限に困難なことだろうと、私は思うのです。.....」
『バークレー司教：解析者より』
「そして、この流率（微分）とは何だろうか？
無限小の増分の速度。 そして、これら同じ無限小の増分の速度とは何なんだろうか？
これらは有限の量でもなく、無限に小さい量でもなく、無でもない。 こんなものなら、過ぎ去った量の幽霊と呼んではいけないというのだろうか？ 」
ニュートンとライプニッツの微分は、「無限小」の概念が十分に論理付けされていなかったため、今日のような厳密さが欠けていた。だが、微分は、力学や天文学などで応用可能、しかも実用的であったため、ベルヌーイやロピタル、オイラー、ラグランジュ、ラプラスなどの研究によって普及していった。
微分学が厳密性を伴うようになったのは、19世紀に入ってからである。仏の数学者コーシーは、1821年に発表した「解析教程」で「極限」や「無限小」、「連続関数」の概念を定義し、解析学の基礎を刷新し、その後デデキントやカントールによる実数論などを経て、今日の微分の基礎が完成した。
しかし、この、微分積分が歴史的に持っていたあいまいさとごまかしは、現在の日本の高校の微分積分の教育においては、更にごまかしが拡大されて教えられています。例えば、微分積分学の命綱が「連続関数」の概念ですが、高校数学では間違った定義が教えられています。以下で、その高校教育の実態を見ていきましょう。
連続関数の定義は1817年にBolzanoが中間値の定理を証明する前提条件に連続関数の定義が必要であることを明確にしてから、その定義が定まった。その歴史的経緯から、中間値の定理を成り立たせない関数を連続関数と呼ぶ高校数学での連続関数の定義は偽物である。なお、高校数学で定義された連続関数という言葉が使い物にならないので、大学数学では、連続関数という言葉を使わずに「区間連続」という言葉で本来の意味の連続関数をあらわすことにしています。
【閉区間で連続な関数の最大値・最小値の定理】
閉区間（ ａ≦ｘ≦ｂ）で連続な関数ｆ（ｘ）は、
その区間内で有限の値の最大値と最小値を持つ。
（ここまでが定理）
この定理は、誤った連続関数の定義と異なる、正しい連続関数の定義を前提にした定理です。そのため、この定理は、高校数学では無視することが強いられています。
高校数学では、
ｙ＝１／ｘは、ｘ＝０以外の、全ての定義域の点で連続なので「連続関数」と呼ばれています。
また、高校数学では、閉区間（ ａ≦ｘ≦ｂ）とは、変数ｘの値の範囲を限定する式のことであるという間違いが教えられています。
その誤った知識に基づくと、
【閉区間で連続な関数の最大値・最小値の定理】とは、
変数ｘの範囲（ ａ≦ｘ≦ｂ）内に関数が連続である定義域を持つ連続関数ｆ（ｘ）は、
その範囲（ ａ≦ｘ≦ｂ）内で有限の値の最大値と最小値を持つ。
（ここまでが定理）
という定理と解釈されます。
この「定理」には以下の反例があります。
関数ｆ（ｘ）＝１／ｘは、
変数ｘの範囲
－１≦ｘ≦１
内に定義域（ただしｘ≠０という定義域）が存在し、
－１≦ｘ≦１
内で定義されているどの点でも連続なので、
連続関数です。しかし、この連続関数ｆ（ｘ）は、
ｘ→０の近くで∞と－∞に発散するので、
有限の値の最大値と最小値を持たない。
（反例おわり）
しかし、この定理の基礎となっている正しい連続関数の定義が高校数学での連続関数の定義とは違うので、これは定理の反例にはなっていません。
（補足１）
微分と積分は，歴史的にも，数学的にも，別々に定義される． 独立して定義されたものが，結びついている。 （日本の高校の微分積分の教科書ではいちばん大切な数学の発見が，次代に伝わらない。）
【積分とは何か】
積分については，ここをクリックした先のｐｄｆファイルにある原教授の以下のコメントが大切です。
---（原教授のコメント開始）---------
積分については高校でも習ってはいるが，その基礎を突き詰めていくといろいろと困ったことがでてくる．
特に 「積分は微分の逆演算」として定義すると，「ある関数 f の積分を求めよ」という問題や「この関数の積分は定義できるか？」という問題でハタと困ってしまう．
（微分して f になるような関数がわからない場合，高校までの知識ではお手上げだ．）
この節では高校までの知識はいったん忘れて，「積分とは何か」「積分をどのように定義すべきか」か ら話を始める．
4.1 積分（定積分）の定義
ということで，まずやるべきは「与えられた関数f(x) に対して，その積分を定義すること」である．
これから見ていくように，かなり広いクラスの関数に対してその積分（定積分）を定義することができる．
定積分を通して不定積分も定義できるので，高校までの知識とのつながりがつくことになる．
・・・
積分の最も素朴な定義はこれから紹介する「リーマン和」に基づくもので、、、
---（原教授のコメントおわり）------
（補足２）
（「リーマン積分可能」の定義）
「微分積分学入門」（横田 壽）の１２４ページから１２５ページに「リーマン積分可能」の定義が書いてあります：
（この本は書店で購入できます。）
その他に、高校２年生が勉強するのに適切な、書店で購入できる微分積分の参考書は：
「やさしく学べる微分積分」（石村園子） ￥2000円
が内容がわかり易くて良いと思います。
ここではドイツの数学者G.F.B. Riemann (1826-1917) によって示されたRiemann 積分につ いて学んでいきます．リーマン積分による「積分可能」の定義は、全ての種類の「積分可能」の定義の基礎になっています。
f(x) は閉区間[a, b] で定義されているとします．この閉区間[a, b] を次のような点xi(i = 1, 2, . . . , n) でn 個の小区間に分割します．
（a = x0 < x1 < x2 < · · · < xi < · · · < xn = b）
この分割をΔ で表わし， Δxi = xi − xi−1 (i = 1, 2, . . . , n) のうちで最も大きい値を|Δ| で 表わします．
（注目ポイント）
高校数学で教える区分求積法では、区間を細分した部分区間のグラフの高さf(x)を求めますが、そのｘの位置が部分区間の中の特定の位置に固定されています。
その固定をしないで、どの位置のｘでのf(x)を棒グラフの高さにして計算しても良い、
というのがリーマン積分です。
いま，それぞれの小区間[xi−1, xi] のなかに任意の位置に点ξi をとり，Riemann 和 (Riemann sum) とよばれる次の和を考えます．
このとき、
となる実数S が存在するならば，このS をf(x) の定積分(definite integral) といい， f(x) は閉区間[a, b] で積分可能(integrable) であるといいます．また，このS を次のように表わします．
つまり関数f(x) が閉区間[a, b] で積分可能であるということは，分割の仕方および点ξi(i = 1, 2, . . . , n) のとり方に関係なく、各点の関数値の和が一通りに定まるということです．
この定義に従い、関数の積分可能性を以下の様にして調べることができます。
先ず小さな閉区間[a, b] を定めて、
その区間の小区間への分割の仕方および点ξi(i = 1, 2, . . . , n) のとり方に関係なく、各点の関数値の和が一通りに定まる（積分可能）か否かを調べることができます。
（積分が不可能な関数）
下のグラフの関数ｆ（ｘ）のように、どの位置においても関数の極限が存在しない関数があり得ます。
例えば、
ｘが有理数の場合にｆ（ｘ）＝０であって、
ｘが無理数の場合のｆ（ｘ）＝１
という、極限が存在しない関数ｆ（ｘ）などです。
そういう、極限が存在しない関数ｆ（ｘ）を積分して関数Ｆ（ｘ)を得た場合（もし積分できた場合）、その積分により得られた関数Ｆ（ｘ）は微分可能だろうか。
そもそも、微分の計算は極限を求める計算なので、その関数ｆ（ｘ）が積分できても、その積分した関数Ｆ（ｘ）を微分した場合に、元の関数ｆ（ｘ）は（極限値が存在しないので）、微分によっては得られないと考えます。
上図の関数ｆ（ｘ）の変数ｘ＝ｘ１からｘ＝ｘ２までの変数ｘの閉区間をｎ等分して、その区分した部分毎にｆ（ｘ）の値ｆ（ξ）を求めて、その値の和で積分します。
（１）その際に、 変数ｘ＝ξが全て有理数なら、ｆ（ξ）＝０になり、積分結果は０になります。
（２）一方、変数ｘ＝ξが全て無理数√２の有理数倍なら、ｆ（ξ）＝１になり、積分結果は（ｘ２－ｘ１）になります。
（３）ｆ（ｘ）の値ｆ（ξ）の選び方によって結果が変わるような計算の値は定かでは無いので、その様な関数ｆ（ｘ）は積分することができません。
このように、微分積分学では、あらゆる関数に微分積分を行う理論を作ろうとすると、いろいろな難しい問題があることがわかりました。
微分積分学で、難しい問題が生じない関数の範囲を把握して、その範囲内で微分積分の計算をすることで、応用上で微分積分を使い易くできます。
そのため、使い易い関数として、極限が存在し、かつ、連続な「連続関数」（関数ｆ（ｘ）が連続な範囲にｘの定義域を限定した１つながりに連続な関数が連続関数です）を主に扱う対象にし、また、「微分可能性」で関数の種類と、また、関数の変数ｘの定義域内の所定の範囲を定めて、その所定の範囲内だけで微分積分を行うようにします。その範囲内で成り立つ法則を把握して、種々の公式を導き出して使うことで微分積分学を最大限に応用できるようになります。
微分積分学は、微分可能な関数と積分可能な関数を定義して、その種の関数の間で微分したり積分をします。
「関数を積分して、それを微分したら元の関数に戻る」
という、微分積分学の基本定理がありますが、
その定理は、その関数ｆ（ｘ）の積分可能な部分に限り、かつ積分後の関数Ｆ（ｘ)の微分可能な部分に限って成り立つ定理です。
その定理の大前提に、何が微分可能で何が積分可能であるかの定義があります。
（微分積分学の基本定理を厳密に定義すると、「微分積分学の基本定理」という命題は、積分可能条件を記述した命題です）
（微分可能の定義が微分積分学の基本定理を左右する）
微分積分学の基本定理の根底を支えているのが微分可能の定義です。高校数学の微分可能の定義は、変数ｘが開区間(a＜x＜b)で定義された関数f(x)にしか微分可能が定義されていません。そのため、高校数学の範囲内の知識では、開区間(a＜x＜b)で定義された関数 f(x)にしか、微分積分学の基本定理が成り立ちません。
一方、大学数学では、変数ｘが閉区間（a≦x≦b）で定義された関数f(x)の区間の端点x=a,bでも微分可能が定義されています。そのため、大学数学では、閉区間（a≦x≦b）で定義された関数f(x)にも微分積分学の基本定理が成り立つと教えられています。
微分積分を学ぶ者は、「微分可能」と「積分可能」という制限条件を定め、その制限条件を満足する関数を扱うのが微分積分学だと認識することがとても大切です。
しかし、この一番大切な概念を高校２年には教えない。高校３年に至っても「積分可能」の概念を教えていないようです。
しかも、１９９７年からは、日本の高校の数学IIで面積が無定義に用いられという、数学センスを否定する蛮行が行なわれた。そして、関数ｆ（ｘ）のグラフとｘ軸で囲まれる領域の面積を，ｘ方向で微分するともとの関数ｆ（ｘ）になり、面積の微分がｆ（ｘ）となるという本末転倒なことを教えるようになった。
高校数学で教える積分の定義が、微分積分学の基本定理が使っている積分の概念と異なるものになった。それにもかかわらず、異なる概念になった「積分」を同じく積分と呼んで定理を記述して紹介しているため、高校でも教える微分積分学の基本定理が意味不明になった。
しかし、「積分」がそのように定義されるという高校の教科書の記述は嘘です。そのため、微分積分学の基本定理の存在意義があります。
そもそも、積分の概念は、日本の高校の教科書が微分の逆演算で定義しているような狭い貧弱な概念ではありません。積分の概念は、数学の研究対象を微小な部分に分割して研究し、その微小部分を集積した全体にまとめ上げて全体を考えるという、適用範囲が広い概念なのです。
「歴史的に見ても、微分より積分の方がずっと前に出現している。」
現在の高等学校の教科書は，積分の概念の説明を回避している。
数学者の吉田洋ーが以下のようになげいています。
“論証"・論証"とやかましくいっておきながら，微積のところへ来ると，とたんにいいかげんな議論でごまかしている。一ーまた高校ではごまかさざるを得ないだろう。高校数学の目的は生徒のあたまを混乱させることにあるのだろうか。
また、初めて不定積分を教わり積分定数Cを教わる際に、積分定数Cの正しい扱いを教わらず高校生の頭が混乱している様です。
高校数学において、積分定数Ｃを省略した間違った部分積分の公式が教えられています。
また、「従来から、（高校数学での）円弧の面積を使った証明方法は、循環論法であるという指摘はあったが、依然として、教科書の記述が直らないのは、高校数学の七不思議の一つである。」
積分の被積分関数の計算においては、ｘのある値で０になる関数を分母にする、すなわち、そのｘの値で０になる関数で式を割り算する計算が許されています。しかし、（大学で初めて学ぶ）広義積分を知らないと、その計算が何故許されるかが理解できません。
このようなデタラメな教育では、高校生に微分積分が分からないのも無理無いと考えます。
バークレー司教が、これを知ったら、「論外の教育だ」 と酷評すると思います。
（補足３：日本の微分積分の教育）
ヨーロッパやアメリカでは、「高校で微分積分を教えるのは、直感にうったえる内容に限られ、正確な微分積分を教えられない」という理由で、微分積分は大学生に教える科目になっています。
日本の大学でも、その欧米の教育に合わせて、初めて学ぶ者に分かるように微分積分を改めて教育しているようです。
大学で使う微分積分の参考書は、高校で教える微分積分の知識を全く知らない学生に理解できるように書かれています。
しかも、大学生向けの微分積分の参考書の方が、日本の高校生向けの微分積分の参考書よりやさしく分かり易い。
高校の微分積分を勉強するなら、先ず、大学生向けの微分積分の参考書を読むことを推薦します。高校の微分・積分の教科書は分かりにくいだけで無く、間違いも含まれています。読まない方が良いのではないかと考えます。
とりあえず、高校２年生が勉強するのに適切な、書店で購入できる微分積分の参考書：
「やさしく学べる微分積分」（石村園子） ￥2000円
が内容がわかり易くて良いと思います。大学１年生向けの参考書ですが、高校の微分積分の参考書よりも分かり易い。しかも、ごまかしが無く論理が明確なので、初めて微分積分を学ぶ高校２年生が学習につまずくことが無く、一気に読めると思います。
【数学が得意になるということ】
「スタンフォード：本当の答えを見抜く力」（キース・デブリン）
に、スタンフォード大学に入学した大学生に教える「数学移行講座」の教育内容が書かれています。
数学移行講座が必要な理由は、学生が大学の数学教育についていけるようにする基本的考え方を教える必要があるからです。
「数学的能力は２つのタイプに分類できます。
最も必要とされている能力は、２つ目のタイプの能力で、
製造業などで新しい問題に取り組んで、その鍵となる特徴を認識して数学的に記述し、その数学的記述を使って問題を正確に分析することができる能力です。
数学教育では主に１つ目のタイプの人間（公式を覚えて当てはめて定型的な問題の答えを出すことができる）を育てることに力点が置かれてきましたが、結果的に２つ目のタイプの人間も育ちました。
２１世紀は、タイプ２の能力に対する需要の方が大きくなっています。
このタイプ２の人材は、
数学の箱の中ではなく、外で考えられる人材です。
「斬新な数学的思考家」と呼ぶのが良さそうです。
微分積分を学ぶ意味は、この「斬新な数学的思考家」になることにあります。
そのため、学生が「タイプ２」になることを妨害している高校生の微分積分の教科書を捨て、
正確に正しい数学を教えている本：
「やさしく学べる微分積分」（石村園子） ￥2000円
等を手に入れて、その本から微分積分を学ぶと良いと考えます。
なお、高校生になった学生は、心身ともに大人として完成する時期に入ったので、もう中学生時代のように受け身で勉強や生きる道を選択するのでは無く、自分から積極的に広く情報を集めて取捨選択して信頼できる情報を手に入れるようにして欲しいと思います。
世間に流通している情報には、誤った情報の方が多く、正しい情報が少ないです。誤った情報しか手に入らないと、誤った情報は問題解決の役に立たないので自信が無くなり、どうしても受け身で勉強する姿勢になり易いです。
正しい情報の貴重さを認識する経験を積んで欲しいと思います。そして、手に入れた正しい情報に基づいた確信と、生きる勇気を手に入れて、人生の永い道に乗り出して行って欲しいと思います。
リンク：
高校数学の目次
新型コロナウイルス感染対策
ｘ→０の近くで∞と－∞に発散するので、
有限の値の最大値と最小値を持たない。
（反例おわり）
しかし、この定理の基礎となっている正しい連続関数の定義が高校数学での連続関数の定義とは違うので、これは定理の反例にはなっていません。
（補足１）
微分と積分は，歴史的にも，数学的にも，別々に定義される． 独立して定義されたものが，結びついている。 （日本の高校の微分積分の教科書ではいちばん大切な数学の発見が，次代に伝わらない。）
【積分とは何か】
積分については，ここをクリックした先のｐｄｆファイルにある原教授の以下のコメントが大切です。
---（原教授のコメント開始）---------
積分については高校でも習ってはいるが，その基礎を突き詰めていくといろいろと困ったことがでてくる．
特に 「積分は微分の逆演算」として定義すると，「ある関数 f の積分を求めよ」という問題や「この関数の積分は定義できるか？」という問題でハタと困ってしまう．
（微分して f になるような関数がわからない場合，高校までの知識ではお手上げだ．）
この節では高校までの知識はいったん忘れて，「積分とは何か」「積分をどのように定義すべきか」か ら話を始める．
4.1 積分（定積分）の定義
ということで，まずやるべきは「与えられた関数f(x) に対して，その積分を定義すること」である．
これから見ていくように，かなり広いクラスの関数に対してその積分（定積分）を定義することができる．
定積分を通して不定積分も定義できるので，高校までの知識とのつながりがつくことになる．
・・・
積分の最も素朴な定義はこれから紹介する「リーマン和」に基づくもので、、、
---（原教授のコメントおわり）------
（補足２）
（「リーマン積分可能」の定義）
「微分積分学入門」（横田 壽）の１２４ページから１２５ページに「リーマン積分可能」の定義が書いてあります：
（この本は書店で購入できます。）
その他に、高校２年生が勉強するのに適切な、書店で購入できる微分積分の参考書は：
「やさしく学べる微分積分」（石村園子） ￥2000円
が内容がわかり易くて良いと思います。
ここではドイツの数学者G.F.B. Riemann (1826-1917) によって示されたRiemann 積分につ いて学んでいきます．リーマン積分による「積分可能」の定義は、全ての種類の「積分可能」の定義の基礎になっています。
f(x) は閉区間[a, b] で定義されているとします．この閉区間[a, b] を次のような点xi(i = 1, 2, . . . , n) でn 個の小区間に分割します．
この分割をΔ で表わし， Δxi = xi − xi−1 (i = 1, 2, . . . , n) のうちで最も大きい値を|Δ| で 表わします．
（注目ポイント）
高校数学で教える区分求積法では、区間を細分した部分区間のグラフの高さf(x)を求めますが、そのｘの位置が部分区間の中の特定の位置に固定されています。
その固定をしないで、どの位置のｘでのf(x)を棒グラフの高さにして計算しても良い、
というのがリーマン積分です。
いま，それぞれの小区間[xi−1, xi] のなかに任意の位置に点ξi をとり，Riemann 和 (Riemann sum) とよばれる次の和を考えます．
この定義に従い、関数の積分可能性を以下の様にして調べることができます。
先ず小さな閉区間[a, b] を定めて、
その区間の小区間への分割の仕方および点ξi(i = 1, 2, . . . , n) のとり方に関係なく、各点の関数値の和が一通りに定まる（積分可能）か否かを調べることができます。
（積分が不可能な関数）
下のグラフの関数ｆ（ｘ）のように、どの位置においても関数の極限が存在しない関数があり得ます。
例えば、
ｘが有理数の場合にｆ（ｘ）＝０であって、
ｘが無理数の場合のｆ（ｘ）＝１
という、極限が存在しない関数ｆ（ｘ）などです。
そもそも、微分の計算は極限を求める計算なので、その関数ｆ（ｘ）が積分できても、その積分した関数Ｆ（ｘ）を微分した場合に、元の関数ｆ（ｘ）は（極限値が存在しないので）、微分によっては得られないと考えます。
上図の関数ｆ（ｘ）の変数ｘ＝ｘ１からｘ＝ｘ２までの変数ｘの閉区間をｎ等分して、その区分した部分毎にｆ（ｘ）の値ｆ（ξ）を求めて、その値の和で積分します。
（１）その際に、 変数ｘ＝ξが全て有理数なら、ｆ（ξ）＝０になり、積分結果は０になります。
（２）一方、変数ｘ＝ξが全て無理数√２の有理数倍なら、ｆ（ξ）＝１になり、積分結果は（ｘ２－ｘ１）になります。
（３）ｆ（ｘ）の値ｆ（ξ）の選び方によって結果が変わるような計算の値は定かでは無いので、その様な関数ｆ（ｘ）は積分することができません。
このように、微分積分学では、あらゆる関数に微分積分を行う理論を作ろうとすると、いろいろな難しい問題があることがわかりました。
微分積分学で、難しい問題が生じない関数の範囲を把握して、その範囲内で微分積分の計算をすることで、応用上で微分積分を使い易くできます。
そのため、使い易い関数として、極限が存在し、かつ、連続な「連続関数」（関数ｆ（ｘ）が連続な範囲にｘの定義域を限定した１つながりに連続な関数が連続関数です）を主に扱う対象にし、また、「微分可能性」で関数の種類と、また、関数の変数ｘの定義域内の所定の範囲を定めて、その所定の範囲内だけで微分積分を行うようにします。その範囲内で成り立つ法則を把握して、種々の公式を導き出して使うことで微分積分学を最大限に応用できるようになります。
微分積分学は、微分可能な関数と積分可能な関数を定義して、その種の関数の間で微分したり積分をします。
「関数を積分して、それを微分したら元の関数に戻る」
という、微分積分学の基本定理がありますが、
その定理は、その関数ｆ（ｘ）の積分可能な部分に限り、かつ積分後の関数Ｆ（ｘ)の微分可能な部分に限って成り立つ定理です。
その定理の大前提に、何が微分可能で何が積分可能であるかの定義があります。
（微分積分学の基本定理を厳密に定義すると、「微分積分学の基本定理」という命題は、積分可能条件を記述した命題です）
（微分可能の定義が微分積分学の基本定理を左右する）
微分積分学の基本定理の根底を支えているのが微分可能の定義です。高校数学の微分可能の定義は、変数ｘが開区間(a＜x＜b)で定義された関数f(x)にしか微分可能が定義されていません。そのため、高校数学の範囲内の知識では、開区間(a＜x＜b)で定義された関数 f(x)にしか、微分積分学の基本定理が成り立ちません。
一方、大学数学では、変数ｘが閉区間（a≦x≦b）で定義された関数f(x)の区間の端点x=a,bでも微分可能が定義されています。そのため、大学数学では、閉区間（a≦x≦b）で定義された関数f(x)にも微分積分学の基本定理が成り立つと教えられています。
微分積分を学ぶ者は、「微分可能」と「積分可能」という制限条件を定め、その制限条件を満足する関数を扱うのが微分積分学だと認識することがとても大切です。
しかし、この一番大切な概念を高校２年には教えない。高校３年に至っても「積分可能」の概念を教えていないようです。
しかも、１９９７年からは、日本の高校の数学IIで面積が無定義に用いられという、数学センスを否定する蛮行が行なわれた。そして、関数ｆ（ｘ）のグラフとｘ軸で囲まれる領域の面積を，ｘ方向で微分するともとの関数ｆ（ｘ）になり、面積の微分がｆ（ｘ）となるという本末転倒なことを教えるようになった。
高校数学で教える積分の定義が、微分積分学の基本定理が使っている積分の概念と異なるものになった。それにもかかわらず、異なる概念になった「積分」を同じく積分と呼んで定理を記述して紹介しているため、高校でも教える微分積分学の基本定理が意味不明になった。
しかし、「積分」がそのように定義されるという高校の教科書の記述は嘘です。そのため、微分積分学の基本定理の存在意義があります。
そもそも、積分の概念は、日本の高校の教科書が微分の逆演算で定義しているような狭い貧弱な概念ではありません。積分の概念は、数学の研究対象を微小な部分に分割して研究し、その微小部分を集積した全体にまとめ上げて全体を考えるという、適用範囲が広い概念なのです。
「歴史的に見ても、微分より積分の方がずっと前に出現している。」
現在の高等学校の教科書は，積分の概念の説明を回避している。
数学者の吉田洋ーが以下のようになげいています。
“論証"・論証"とやかましくいっておきながら，微積のところへ来ると，とたんにいいかげんな議論でごまかしている。一ーまた高校ではごまかさざるを得ないだろう。高校数学の目的は生徒のあたまを混乱させることにあるのだろうか。
また、初めて不定積分を教わり積分定数Cを教わる際に、積分定数Cの正しい扱いを教わらず高校生の頭が混乱している様です。
高校数学において、積分定数Ｃを省略した間違った部分積分の公式が教えられています。
また、「従来から、（高校数学での）円弧の面積を使った証明方法は、循環論法であるという指摘はあったが、依然として、教科書の記述が直らないのは、高校数学の七不思議の一つである。」
積分の被積分関数の計算においては、ｘのある値で０になる関数を分母にする、すなわち、そのｘの値で０になる関数で式を割り算する計算が許されています。しかし、（大学で初めて学ぶ）広義積分を知らないと、その計算が何故許されるかが理解できません。
このようなデタラメな教育では、高校生に微分積分が分からないのも無理無いと考えます。
バークレー司教が、これを知ったら、「論外の教育だ」 と酷評すると思います。
（補足３：日本の微分積分の教育）
ヨーロッパやアメリカでは、「高校で微分積分を教えるのは、直感にうったえる内容に限られ、正確な微分積分を教えられない」という理由で、微分積分は大学生に教える科目になっています。
日本の大学でも、その欧米の教育に合わせて、初めて学ぶ者に分かるように微分積分を改めて教育しているようです。
大学で使う微分積分の参考書は、高校で教える微分積分の知識を全く知らない学生に理解できるように書かれています。
しかも、大学生向けの微分積分の参考書の方が、日本の高校生向けの微分積分の参考書よりやさしく分かり易い。
高校の微分積分を勉強するなら、先ず、大学生向けの微分積分の参考書を読むことを推薦します。高校の微分・積分の教科書は分かりにくいだけで無く、間違いも含まれています。読まない方が良いのではないかと考えます。
とりあえず、高校２年生が勉強するのに適切な、書店で購入できる微分積分の参考書：
「やさしく学べる微分積分」（石村園子） ￥2000円
が内容がわかり易くて良いと思います。大学１年生向けの参考書ですが、高校の微分積分の参考書よりも分かり易い。しかも、ごまかしが無く論理が明確なので、初めて微分積分を学ぶ高校２年生が学習につまずくことが無く、一気に読めると思います。
【数学が得意になるということ】
「スタンフォード：本当の答えを見抜く力」（キース・デブリン）
に、スタンフォード大学に入学した大学生に教える「数学移行講座」の教育内容が書かれています。
数学移行講座が必要な理由は、学生が大学の数学教育についていけるようにする基本的考え方を教える必要があるからです。
「数学的能力は２つのタイプに分類できます。
最も必要とされている能力は、２つ目のタイプの能力で、
製造業などで新しい問題に取り組んで、その鍵となる特徴を認識して数学的に記述し、その数学的記述を使って問題を正確に分析することができる能力です。
数学教育では主に１つ目のタイプの人間（公式を覚えて当てはめて定型的な問題の答えを出すことができる）を育てることに力点が置かれてきましたが、結果的に２つ目のタイプの人間も育ちました。
２１世紀は、タイプ２の能力に対する需要の方が大きくなっています。
このタイプ２の人材は、
数学の箱の中ではなく、外で考えられる人材です。
「斬新な数学的思考家」と呼ぶのが良さそうです。
微分積分を学ぶ意味は、この「斬新な数学的思考家」になることにあります。
そのため、学生が「タイプ２」になることを妨害している高校生の微分積分の教科書を捨て、
正確に正しい数学を教えている本：
「やさしく学べる微分積分」（石村園子） ￥2000円
等を手に入れて、その本から微分積分を学ぶと良いと考えます。
なお、高校生になった学生は、心身ともに大人として完成する時期に入ったので、もう中学生時代のように受け身で勉強や生きる道を選択するのでは無く、自分から積極的に広く情報を集めて取捨選択して信頼できる情報を手に入れるようにして欲しいと思います。
世間に流通している情報には、誤った情報の方が多く、正しい情報が少ないです。誤った情報しか手に入らないと、誤った情報は問題解決の役に立たないので自信が無くなり、どうしても受け身で勉強する姿勢になり易いです。
正しい情報の貴重さを認識する経験を積んで欲しいと思います。そして、手に入れた正しい情報に基づいた確信と、生きる勇気を手に入れて、人生の永い道に乗り出して行って欲しいと思います。
リンク：
高校数学の目次
新型コロナウイルス感染対策
（７）
（９）
