「微分・積分」の勉強
高校2年生から、極限・微分・積分の「意味がわからない」「つまらない」「教わる計算方法が正しいと言える理由(証明)がわからない」で数学の学習から脱落する高校2年生が多いらしい。
その脱落の原因を考えます。
脱落する原因は、微分積分には歴史的に説明のあいまいさがある事、そして、日本の高校の微分積分の教育では、そのあいまいさを更にあいまいにして、異なる事を同じことだと言って説明を単純化したり、証明が難しい事は証明しないで、それが証明されたと感覚的に感じるようごまかして教え、その説明のおかしさに生徒が気付かないよう生徒の数学感覚を麻痺させるよう誘導している事が、脱落の原因だと思います。また、そのように数学感覚が麻痺したまま大学に入ると、大学で学ぶ正しい微分積分が全く理解できなくなります。
ごまかしのある説明をするように指示された先生は、説明にごまかしがある事を知っています。そして、その説明を論理的に詳しく説明すると、ごまかしが白日の下にさらされるので、説明の論理性を追求する事を嫌います。そのため、ごまかしを教える先生は、生徒に徹底した説明ができず、説明する事自体を避ける事になります。
生徒に微分積分を完全に理解できる必須な公式を全部教えると、それも、ごまかしを白日の下にさらす種になるので、必須公式を全部教える事も避けられていると考えます。
公式を生徒に覚えさせるときに、間違ってはいるが覚えやすい事を生徒に覚えさせる事が、微分積分を生徒にやさしく覚えられるようにした親切な教育である、といった誤解があるから、教わる高校生が混乱することが原因で生徒が脱落するのではないかと考えます。
ごまかしがある説明は、どう説明しても、論理的には筋が通りません。論理的には理解され得ない事ですので、数学センスのある学生には受け入れられず、それ以上一歩も前に進めなくなると思われます。
数学の公式を覚える数学センスから考えると、嘘とごまかしは、数学を覚えにくくするので禁物なのです。なぜかと言うと、数学の公式を覚えるというのは公式を導き出す小さなヒントだけ覚えて、そのヒントから公式全体を導き出せるようにすることだからです。
小さなヒントだけ覚えれば良いので多くの公式を覚える量が本当に少なくて済み、覚えるのが楽になります。
しかし、嘘とごまかしによっては、そこから正しい公式全体を導き出せ無くなります。そのような不純物(嘘、ごまかし)が心に入ると、もう数学の力は失われてしまい、何もわからなくなります。そのため、数学センスのある学生には、嘘とごまかしは受け入れられないのです。
数学センスのある学生が学習を一歩も前に進めることができなくなることが無い、安心して微分積分の勉強を進めることができる、ごまかしの無い本は、高校生用の教科書や参考書なのでは無く、大学1年生向けの参考書:例えば:「やさしく学べる微分積分」(石村園子) ¥2000円 などだと思います。その本は、微分積分を初めて学ぶ高校2年生にとって、内容がわかり易くて、しかも正確であって良いと思います。その本の36ページから45ページまで勉強するだけで、微分の必須知識が学べます。
なお、その本から学んだ本物の微分積分の知識は、高校の微分積分の教義から見れば異端の知識です。そのため、それを知っていることを隠してください。
ガリレオ・ガリレイが「太陽が地球の周りを回っているのでは無く、地球の方が動いている」と言ったときにどのような目にあったかの歴史を学んでください。
くれぐれも、授業中に、先生や生徒が間違った微分積分の計算をしたときに、その誤りを指摘したりしないように、慎重に、周りの空気を読んで行動してください。ただし、その誤りは、大学入学試験には通用しませんが、、、
当ブログでは、数学センスのある学生にも微分積分がわかるように、ごまかしの無い微分積分の解説をするようにします。
(微分積分を使いものにする言葉について)
数学者の小平邦彦「[軽装版]解析入門Ⅰ」では、微分積分を使いものになる道具にするため、数学の定理で連続関数を使うときに必ず使う形に整合させて連続関数を定義しています。すなわち、連続関数という言葉を、連結区間で1つながりに連続する関数と定義しています。
また、使いものにならなくなっている「不連続点」と言われている言葉を使わず、微分積分の概念の理解のために役立つ言葉で、連続点以外の点をあらわす「連続で無い点」という言葉を使っています。そのため、当ブログでも、小平邦彦「[軽装版]解析入門Ⅰ」に従って、「不連続点」という言葉は使わず、「連続で無い点」という言葉を使います。
(不連続点の当初の定義も、連続で無い点の定義と同じでした。藤原松三郎の「微分積分学 第1巻」によると、「f(x)がx=ξで連続でない場合に、x=ξをf(x)の不連続点という。」と定義されていました。)
高校2年の微分積分の勉強のためには、「やさしく学べる微分積分」(石村園子)を読んで、高校3年になって本格的に微分積分を学びたくなった学生は、学生が微分積分を無駄なく学べるよう工夫がこらされている本:小平邦彦「[軽装版]解析入門Ⅰ」を読むと、微分積分が無駄なく勉強できて良いと思います。
なお、それらの本から学んだ本物の微分積分の知識は、高校の微分積分の教義から見れば異端の知識です。そのため、それを知っていることを高校では隠してください。大学入学試験の答案に書くのはもちろん良いですが、、、
高校では、定積分を以下のように教えています。
【関数f(x)の定積分を以下のように定義する】
(1)微分したらf(x)になる関数F(x)を見つけること。
この関数F(x)を原始関数と呼ぶ。

この原始関数を使って、以下の計算で定積分する。
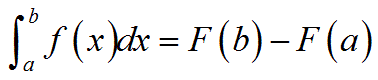
【問題点】
数学センスを持つ人が知っている以下の常識があります。
『 「何かAが存在するならば、それで何かBができる」という定理であって、
その存在する「何かA」の集合がどういうものであるかが示せない、
言い換えると、その定理がいつ使えて、いつ使えないかを示せない、
という定理には、定理としての価値が無い』と言う常識です。
なぜなら、その定理(命題)を等価な命題である「対偶」に言い換えると、
『何かBができないならば、何かAが存在しない。何かBができた場合は、何かAが存在するかしないかは分からない』
となります。この命題は、何かBができるための前提条件を教えてはいません。そのため、この命題は「何かB」の本質を教える情報は含んでいないし、また、「何かA」の本質を教える情報も含んでいません。定理の要素がおぼろげながら見えてきた段階で、その要素の関係をしっかり調べた定理にはせずに、とりあえず「定理」にした未完成な形の定理になっています。
この様な表現の他の例として、例えば以下の「定理」:
「関数f(x)にxを掛け算した関数をF(x)とする。このとき、F(x)の微分がf(x)となる関数F(x)が存在するならば、その関数F(x)がf(x)の積分である」
という「定理」には価値が無い。
f(x)=1の場合
F(x)=xとなり、たしかにこの「定理」が成り立っている。
f(x)=xの場合、
F(x)=x2となり、
F’(x)=2x≠f(x)なので、この定理が規定する存在条件を満足する関数F(x)が無い。
よって、この場合も、この定理には矛盾がない。
しかし、この論理には大きな欠陥があります。
「言っていることが成り立つ場合に、その定理が使える」
という条件を加えた定理は、いつだって成り立ちます。なぜならば、成り立たない場合は、その定理の適用範囲外だと規定しているからです。
この「定理」は、いつ使えるかを明確化した定理に書き換えることができ、その書き換えた定理は:
「関数f(x)にxを掛け算した関数をF(x)とする。関数f(x)が定数である場合に限り、その関数F(x)がf(x)の積分である」
というように、内容を明確化して書き換えることができます。
このように、いつ使えるかを明確化してみると、元の「定理」は、いつ使えて、いつ使えないかを定義せずあいまいにしている「ごまかし」があっただけとわかります。定理は、このように明確化しなければなりません。
そのため、いつ使えて、いつ使えないかを定義していない定理は、
解くべき問題(いつ使えて、いつ使えないかという問題)を解かずに、
問題をあいまいにしている「ごまかし」があるので、
定理としての価値がありません。
【関数f(x)の定積分を以下のように定義する】では、原始関数F(x)が存在すれば、という適用除外条件があり、しかも、その適用が除外されない、存在するF(x)とはいかなるものかということが定義されていないので、無価値な定義です。
【不正確な情報から真実を見抜くコツ】
以下で説明するように、高校で教わる原始関数の定義は(大学での定義とは異なり)不正確なあいまいな定義です。
そのように、不正確な情報から真実を拾い出すコツがあります。それは、扱う関数を均質な基本的な要素に分割して、その分割された関数に不正確かもしれない情報を適用します。
具体的には、関数を、全て、1つながりに連続する関数に分割して考えます。その、1つながりに連続する関数を扱うのであれば、不正確な情報の公式を適用したとしても誤りに陥る事を防ぐことができます。
そのように、先ずは、1つながりに連続する関数毎に積分を調べれば良いのです。
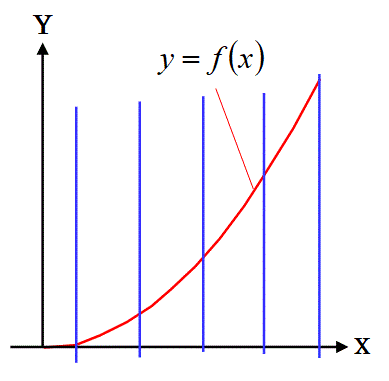
例えば、下図の関数f(x)を考える場合:
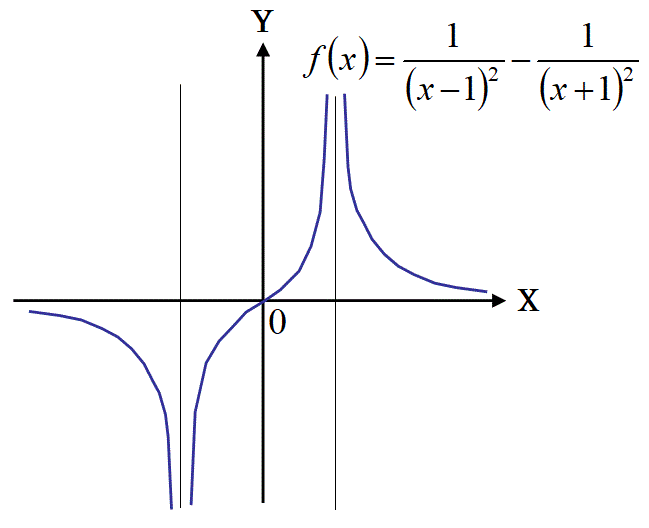
x<-1での1つながりに連続する関数と、
-1<x<1での1つながりに連続する関数と、
1<x での1つながりに連続する関数を、
別々の3つの関数と考えれば良いのです。
そのように、関数全体を、均質な基本的な要素の関数に分割して、その基本要素だけに公式を適用すれば、不正確な壊れた道具の定理(例えば正しい原始関数の定義を使って証明した定理を作ってから、原始関数の定義を変えてしまって、その定理を適用するという使い方の定理)を使いこなすことができるようになります。
不正確な情報が与えられても正しい答えを出せるようになる事は、数学の極意を習得するという事でもあり、大事な数学的分析態度だと考えます。
【原始関数とは何か】
先ず、原始関数の正しい定義が何であるかという事から話を始めなければなりません。
【原始関数の誤解される定義】
関数F(x)の定義域がわからない定義:
ある関数F(x)を微分すると、
F’(x)=f(x)
になるとき、関数F(x)を関数f(x)の原始関数と呼ぶ。
(原始関数の定義おわり)
【原始関数の正しい定義】
上の定義は、誤解されるあいまいな不正確な定義であり、原始関数F(x)の定義域がどの領域かが示されていない(定義域が決まらなければ関数が定義されない)、明確さを欠いているので、まともな定義とは言い難いものです。
正確な当初の原始関数の定義は:
関数F(x)が、連結区間a<x<bのどの点でも連続、かつ、微分可能な関数であれば、F(x)を微分して導関数f(x)が求められる。この場合に、F(x)を関数f(x)の原始関数と言う、
と定義されていました。
(藤原松三郎の「微分積分学 第1巻」)
定義4.25.
閉区間[a, b] で定義された関数f が与えられたとき,
(a≦x≦bとなる全ての実数のxに対して有限の値のf(x)が定義されている。)
f を導関数に持つ関数F が存在すれば,
(F(x)が、a≦x≦bの全領域でF’(x)=f(x)であるとは、全領域で微分可能ということであり、それゆえ、F(x)はa≦x≦bで連続な関数。)
F をf の原始関数と呼ぶ.
(名古屋大学教授 内藤久資の講義ノート(4))
この定義も、原始関数F(x)は、定義域の連結区間内のどの点でも連続、かつ、微分可能な関数であって、それを微分した導関数がf(x)になる関数、と定義している。
すなわち、原始関数はその定義域の連結区間における連続関数であり1つながりのグラフであると定義されています。
《区間という用語の意味》
また、「区間」という数学用語は、実数の集合として定義されている用語である事に注意が必要です。
a≦x≦bを満足するxの区間という表現は、a≦x≦bの範囲内の全ての実数xという意味です。
-∞<x<∞という区間もあります。
区間はxの値の範囲を限定するためのa≦x≦bという式とは意味が異なることに注意する必要があります。
区間a≦x≦bが命題の中に記載されている場合は、その範囲内の全ての実数xについて命題を検討する必要があります。被積分関数f(x)が定義されていない変数xの点があっても、その点も、その命題が検討されるべき点の1つです。
小平邦彦「[軽装版]解析入門Ⅰ」の164ページでも:
「ある(連結)区間Iで定義された関数f(x)が与えられたとき、f(x)を導関数とする関数、すなわち、F’(x)=f(x)なる(連結区間)Iで定義された関数F(x)をf(x)の原始関数という。」
と定義されています。
すなわち、原始関数は連結区間で連続な関数であり1つながりのグラフであると定義されています。
高校生に積分を正しく教えるサイトでの原始関数の定義:
「 f(x) を実数上の連結区間で定義された関数とする.このとき,同じ連結区間上の関数で, F′(x)=f(x) を満たす関数 F(x) を f(x) の原始関数と言う。」
このサイトの定義でも、原始関数は連結区間における連続関数であり1つながりのグラフであると定義されています。
推薦できる高校数学の参考書:「生き抜くための高校数学」(芳沢光雄)でも、原始関数を、
「ある(連結)区間で定義された(被積分)関数f(x)に対し、F’(x)=f(x)となる関数F(x)があるとき、F(x)をf(x)の原始関数という。」
と定義しています
この参考書の定義でも、原始関数は連結区間における連続関数であり1つながりのグラフであると定義されています。
(注意)
F(x)が微分可能でF'(x)=f(x)であっても、f(x)が連続関数になるとは限らないことに注意。F(x)が連続であっても微小に振動している場合があるからです。そのため、連続関数で無いf(x)に原始関数F(x)がある場合もある。
(原始関数の例)
下図の関数f(x)の原始関数F(x)を考える。
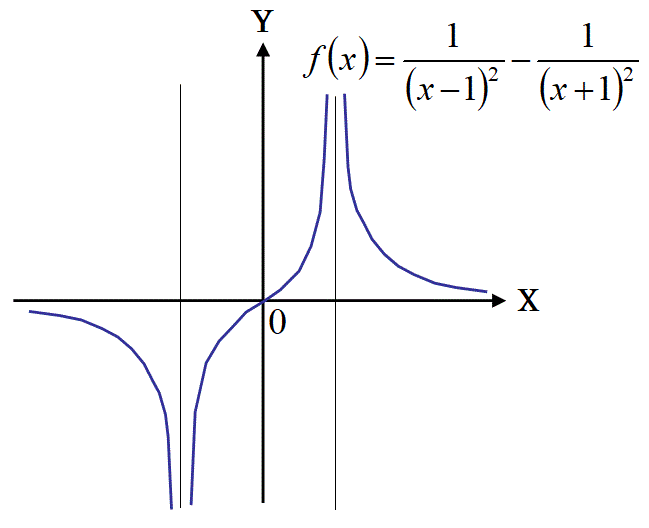
上図の関数f(x)の原始関数F(x)は、下図の様に3つある。
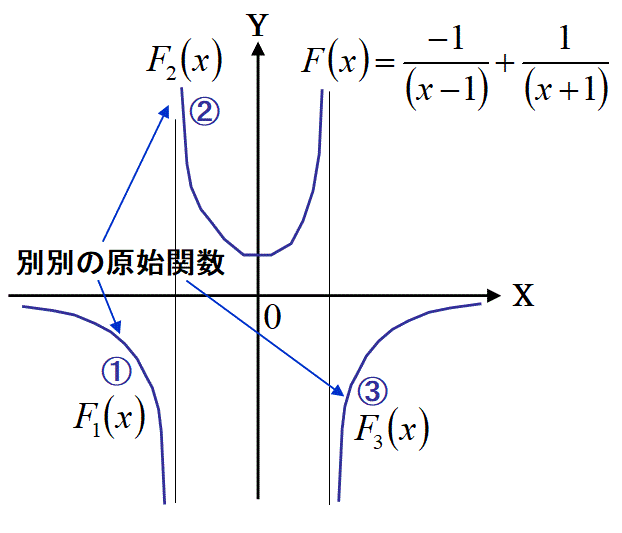
1つながりのグラフが1つの原始関数です。その他のグラフは別の原始関数です。上図の様に3つの別々の原始関数があります。
(あいまいな原始関数の定義の問題点)
ある関数F(x)を微分すると、F’(x)=f(x)
になる、というだけの定義なら、その定義を厳密に適用すると、
関数F(x)の定義域が分断されていても、その分断された各定義域において、
F’(x)=f(x)
となる関数(補足1の誤解された原始関数)の全部の分断された定義域をまとめて定義域にした関数も原始関数になってしまいます。
高校生は、原始関数の誤った定義に従った以下の補足1の誤解された原始関数を、真の原始関数に係る公式に適用することで、間違った答えを出す矛盾に直面します。
(補足1)
F(x)=1/xをxで微分したらf(x)=-1/x2になるので、関数f(x)の原始関数がF(x)=1/xです。
なお、F(x)=1/xは、x=0では関数F(x)が定義されず、関数が定義されているどの点で微分しても、結果が全てf(x)=-1/x2になるので、間違いなく、F(x)はf(x)の原始関数であると誤解します。
(不連続な、誤解された原始関数の特徴)
ただし、不連続な誤解された原始関数の場合は、異常な原始関数になり、例えば、
x>0で、F(x)=1/x+3,
x<0で、F(x)=1/x+100,
という、
先の原始関数の連続で無い点で分離された領域毎に異なる定数を加えて作った原始関数であっても、
f(x)=F’(x)=-1/x2
になります。
つまり、同じf(x)の誤解された原始関数群が、1つの誤解された原始関数F(x)+Cという形だけでは表しきれません。
このことを、もっと単純化して考えてみます。下のグラフのように、点x=0で不連続な誤解された原始関数F(x)を考えると理解し易いと考えます。

この誤解された原始関数F(x)が、x≠0において、
dF(X)/dx=f(x)=0
となります。
被積分関数f(x)が、
x=0ではf(x)の値が定義されず、
f(x)=0 (x>0)
f(x)=0 (x<0)
という関数である場合において、
f(x)に対する誤解された原始関数F(x)は:
F(x)=C1, (x>0)
F(x)=C2, (x<0)
という、2つの定数C1とC2を使った解が得られる事を考えると理解し易くなると考えます。
この2つの異なる積分定数毎に関数を異ならせる事ができるので、異なる積分定数が設定できる部分毎に異なる関数があり、それらを一緒にして1つの関数としてはいけないと考えられます。
この1つになった原始関数は、定義域がx<0とx>0であって、その定義域の中に連続で無い点を含みましたが、積分を行う際に必要な、真の原始関数F(x)は、変数xの連結区間の中に関数F(x)が連続で無い点を含まない原始関数です。
誤解された原始関数F(x)は、
連続で無い点で分離される、異なる積分定数が設定できる領域毎に、独立に、
F(x)+C
というように、1つの積分定数だけで置き換えられて、微分すると同じf(x)が得られる部分を、f(x)の1つの正しい原始関数であると解釈できます。
この積分定数Cは、
誤解された原始関数F(x)のうち、連続で無い点で分離された正しい原始関数毎に1つの積分定数を使う事ができるのです。
(真の原始関数は、誤解された原始関数F(x)の連続で無い点で分離された領域の1つを定義域とする関数です。)
誤った定義に従った補足1の誤解された原始関数と、原始関数の性質として教えられる公式とが違っている矛盾を見せられた高校生が微分積分の理解に苦しむのは当たり前の事と思います。
なぜなら、原始関数の定義が誤っているので、正しい原始関数の概念を使ったあらゆる公式が無意味な公式になります。そして、それらの無意味になった公式を使ったあらゆる公式が無意味になるからです。
このような嘘を押し付けられ覚える事を強制され、微分積分がわからないようにされている高校生に心から同情します。
(補足2)
また、関数はその定義域とセットにして定義され、定義域が異なれば異なる関数であると区別されるものなので、
先ずは、定義域を広くした”原始関数F(x)”を考えて、その定義域を関数f(x)の定義域にまで狭くした関数F(x)をf(x)の真の原始関数F(x)と考えると良い。
そうする方が原始関数の発見方法としてわかりやすく実用的と考えます。
【不定積分とは何か】
定積分の計算については、
連結区間a≦x≦bの全ての点で関数f(x)が連続であれば、
以下の不定積分F(x)を使った計算でその区間の定積分が計算できる。
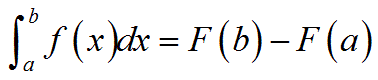
連結区間a≦x≦bの全ての点で関数f(x)が連続の場合は、不定積分F(x)が求められて上式で定積分が計算できるが、
連結区間a≦x≦bに中に関数f(x)が連続で無い点がある場合に、不定積分と思ったF(x)を上の式に使って定積分を計算すると答えが間違う。
という定理(微分積分学の基本定理)があるだけです。
(微分積分学の基本定理の詳細)
関数y=f(x)が、 連結区間a≦x≦b の全ての点で連続とする。 その条件が成り立つならば、必ず、
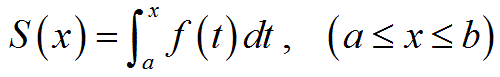
という計算をすることができる。
そして、次のことが成り立つ。
(1)S(x)はf(x)の不定積分(=実用的原始関数)である。
(S(x)は、必ず1つながりの連続関数になる。)
このS(x)の式はf(x)の不定積分の定義になっています。
不定積分S(x)は、連結区間a<x<bのどの点でも、
S'(x)=f(x)
になるので原始関数でもあります。
(注意)
以下の関数f(x)は関数の定義域内の全ての点で連続ですが、1つながりに連続な関数では無いので連続関数ではありません。
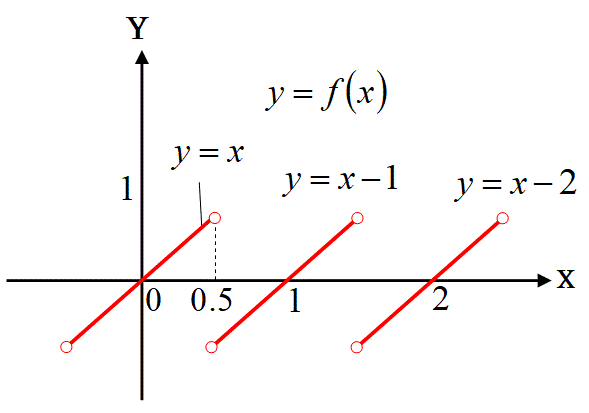
この切れ切れのノコギリ状の関数f(x)を積分した関数F(x)を求めてみます。
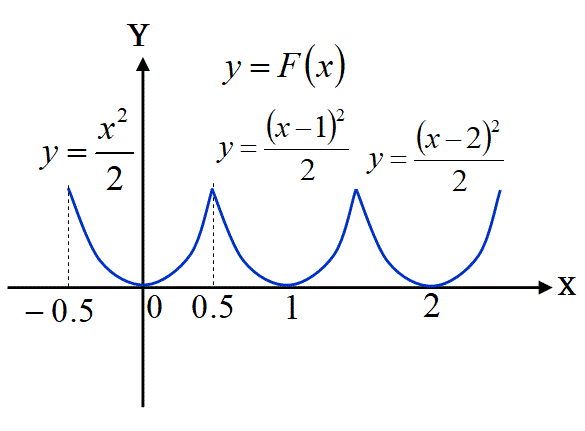
この関数F(x)を微分すると、x=0.5, 1.5, 2.5等では、F(x)の微分係数が計算できません。
この関数F(x)は原始関数ではありません。
それは、f(x)が1つながりに連続では無いので連続関数では無いからです。
高校生は教科書から、誤った連続関数の定義:
「関数 f(x) が、定義域のすべての x の値で連続であるとき、 f(x) は連続関数である。」
を教わることで、
正しい定理:「連続関数を積分した式はすべて微分可能である」が、
その誤った連続関数の定義から導かれるこの反例によって否定されてしまうという問題に直面します。
こういう問題に直面する高校生に心から同情します。
(注意おわり)
この不定積分S(x)(=原始関数)は、
大学以上になると、
積分の閉区間の端部x=a,bでも、
片側微分係数だけがあれば、微分可能であるとして、
端点での微分係数が定義されています。
(2)F(x)を、
a≦x≦b 上で連続な関数f(x)の任意の不定積分(=実用的原始関数)とすると、

が成立する。
この式では不定積分F(x)を使って計算するが、被積分関数f(x)がa≦x≦bで連続な関数である場合は、この式に原始関数を使っても良い。
(定理の定義おわり)
すなわち、この微分積分学の基本定理によって、
関数f(x)がa≦x≦b上で連続であるならば、
不定積分S(x)やF(x)が、f(x)のその範囲内の積分で計算する事で求められる事が保証されています。
そうして計算して得た不定積分F(x)、(定義域で連続な原始関数)、を使って、
関数f(x)が連続である範囲のa≦x≦bでの定積分を、
F(b)-F(a)で計算できる事が保証されています。
-----(注意)---------
(積分の特徴)
積分は、関数f(x)のグラフの面積を求める計算です。グラフの多くの部分の総和の面積を求めるものです。そのため、グラフの微小な一部分の過不足があっても総体の面積に対する影響はわずかです。例えば、グラフの1点の値f(0)が何であっても(ただしf(0)が無限大で無ければ)、総体の面積に対する影響は0であると言えます。
そのため、積分では、グラフの微小部分には注目しないで計算をします。
そのため、被積分関数f(x)の不定積分F(x)が、以下のような物であっても、問題にしません。
例えば以下の式の様に、
x=0で不連続な関数f(x)について:
(例えば、f(0)=0,x>0でf(x)=1)

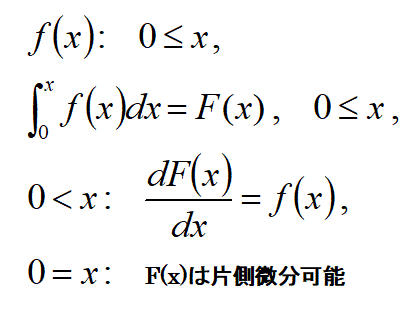

大学以上になると、閉区間の端点x=0において、不定積分F(x)の右微分係数F’+(0)が存在すれば、それをその端点x=0の微分係数であると定義しています。
上の例の不連続関数f(x)の不定積分F(x)の場合は、
F’+(0)=f(0+)(=右側のf(x)の極限)=1
でF(x)の端点x=0での微分係数の値が1になります。
しかし、その微分係数は、元の関数f(0)=0にはなりません。
そのため、得られた不定積分F(x)は被積分関数f(x)の原始関数ではありません。
(積分の本質)
しかし、このことが問題だと考えるのは、積分の本質から外れた発想です。
積分の目的は、不定積分を求める事であって、原始関数を求める事では無いのです。
本当の数学では、使えそうに思った原始関数を試しに微分してf(x)の一部分と比較して、一部分が一致すれば、
その一致した範囲を定義域にした原始関数を不定積分F(x)の一部分の定義域に使って、不定積分F(x)の全体の定義域の関数を求める助けにしているだけなのです。
しかし、高校数学では、そういう手段で使っているだけの脇役の原始関数をことさら強調して、原始関数を主役にしてしまっている本末転倒な事を教えています。しかも、その原始関数の定義も不正確で結果的に嘘が教えられています。
推薦できる高校数学の参考書:「生き抜くための高校数学」(芳沢光雄)では、積分を、不定積分を主役にして説明しています。
積分の特徴は、
不定積分F(x)の微分によってf(x)の1点であるf(0)が再現できないという不定積分であっても、その不定積分F(x)を使って被積分関数f(x)の定積分を計算するには支障がありません。
そういう不定積分の関数F(x)をf(x)に対して求めるだけで充分なのです。
そういう、微分して変数x=0という
1点のf(0)が得られないが、その他の大部分のxでf(x)が微分によって得られる元になる不定積分F(x)を求めれば、それで良いのです。
上図のグラフのf(x)の積分をしようとして、原始関数が得られないから答えが出ないというのは、あまりにお粗末な解き方と思います。
上図のf(x)の原始関数が得られなかったのでは無く、f(x)の定積分に使える不定積分F(x)の解が得られたのです。
不定積分F(x)は、いわば実用的原始関数と呼んで良いと考えます。
なお、原始関数F(x)の定義は、連結区間を定義域にする関数であって、F’(x)=f(x)となり、
その連結区間の全てのxにおいてf(x)が存在する関数です。
しかし、実用的な原始関数と言える不定積分F(x)は、不定積分の定義域の大部分のxで、その式が成り立つだけで良く、端点では式が成り立っていなくても良いのです。そのため、F(x)の微分によってf(0)が求められ無くても実害がありません。
求めるべきなのは不定積分F(x)(=実用的原始関数)です。そのF(x)の定義域の大部分のxでF(x)の微分がf(x)になれば良く、積分への影響が0である数点のxの値でF’(x)がf(x)と一致しない事は無視します。
(不定積分の例)
以下の図の関数f(x)のグラフを考えます。

この関数f(x)の、
-1≦x≦3
の閉区間を小区間に細分した各小区間での関数の値の和が一通りに定まるので、リーマン積分可能です。
この関数f(x)をリーマン積分して、以下の図の不定積分の関数F(x)を求めることができます。
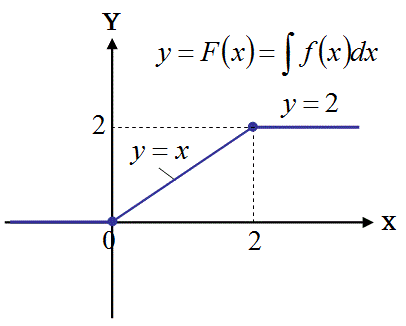
この関数F(x)は、x=0とx=2で微分不可能ですので、原始関数ではあらわせず、原始関数では、上図の様な簡単なグラフの面積を求める事もできません。
しかし、不定積分の部分に原始関数を組み込んで不定積分を作るために原始関数を使うことができます。
上の関数の例では、定義域が0<x<2の範囲のf(x)に対して、定義域が0<x<2である原始関数F(x)が存在します。それを不定積分に組み込みます。また、定義域が2<xの範囲のf(x)に対して、定義域が2<xである原始関数F(x)が存在します。また、定義域がx<0の範囲のf(x)に対して、定義域がx<0である原始関数F(x)が存在します。その3つの原始関数を組み込んで不定積分を作れば良いのです。
【閉区間の端点での微分の注意】
なお、大学以上では、以下の様な拡張された微分の定義が使われます。
閉区間で連続な関数F(x)を閉区間の端点でも微分可能とする拡張された微分の定義が、大阪大学の教授が書いた「微分積分学」(難波誠)の、44ページに記載されています。
閉区間の端点で関数F(x)が片側微分可能であれば、その片側微分を端点での微分係数と定義しています」
そして、閉区間で連続な関数F(x)を端点以外で微分してf(x)を再現できるという確認ができた関数F(x)が、閉区間の端では、この定義の片側微分によりf(0)も再現できた場合に、F(x)がf(x)原始関数であるという説明がされています。
この微分の定義「端点で関数F(x)の微分を片側微分係数で定義する」は大学生以上で使われています。
------注意おわり-------------
(関数が連続で無い範囲で定積分が計算できない例の図)
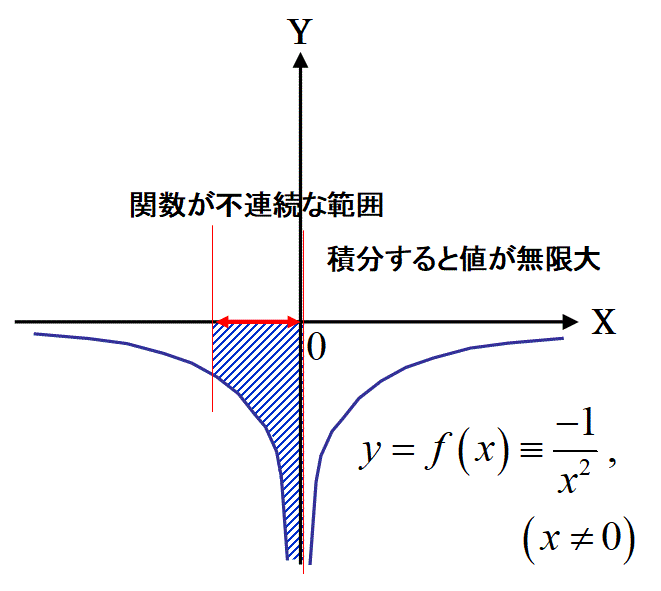
上図の関数を、上図の様にx=0を含む区間で定積分したら、マイナスの無限大になるので、積分が不可能です。例えば、上図の関数をー1から1までの区間で積分する事も(関数f(x)が不連続になるx=0を含む区間で定積分する事になるので)不可能です。
このように積分できない範囲があります。
これを無視して、関数f(x)の連続で無い点を定積分の範囲内に入れてしまうと以下の間違いをおかします。
F(x)=1/xをxで微分したらf(x)=-1/x2になるので、関数f(x)=-1/x2の原始関数がF(x)=1/xである。
しかし、積分区間を、f(x)が不連続になる変数値x=0を含めた、xが-1から1までの区間にして、定義域を広げる事でF(x)を誤解された原始関数にしてしまって、
関数f(x)を定積分しようとして、
その区間で不連続な誤解された原始関数を使って、
F(1)-F(-1)=1-(-1)=2
という 計算をすると、明らかに間違えます。

上の図で明らかな様に、-1から1までの範囲でのf(x)の積分の結果は(積分がグラフの面積を表すので)、マイナス無限大にならなければなりません。
しかし、上の計算はそれと全く違う、間違った答えになったのが明らかです。
(誤解された原始関数の差で計算するから間違えるのであって、不定積分(定義域内で必ず1つながりに連続な関数になる)の差で定積分を計算するならば、この様な間違いは起きません)
なお、
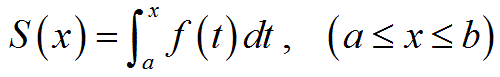
という計算で得た関数S(x)は不定積分であって、1つながりのグラフになります。
実際、a>0の場合には、x>0の範囲の定義域だけの関数
S(x)=1/x, (x>0)
だけが得られます。
a≦b<0の場合には、x<0の範囲の定義域だけの関数
S(x)=1/x, (x<0)
だけが得られます。
a=0の場合には、s(x)が計算できません。
このように積分の式で定義される(定義可能な)不定積分:
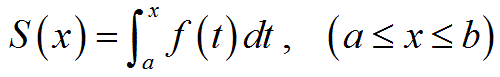
は必ず連続関数になります。
(不定積分の関数は端点x=a,x=bを持つ連結区間で1つながりに連続する関数です)
この不定積分S(x)は、x≠0における誤解された原始関数:
F(x)=1/x, (x≠0)
(これは、定義域がx≠0で、x<0の部分とx>0の部分を両方とも定義域に持つ不連続な誤解された原始関数F(x) である)
とは異なります。
《もう1つの関数の例》

(誤解された原始関数の計算)
上の関数の例では、点x=0で不連続な関数F(x)が、x≠0において、
dF(X)/dx=0
となるとき、
F(x)=C1, (x<0)
F(x)=C2, (x>0)
という、2つの定数C1とC2を使ってあらわされ、そのF(x)の微分がf(x)になるので、このC1とC2で定義された関数F(x)も、f(x)の誤解された原始関数です。
(不定積分の計算)
一方、関数f(x)を不定積分すると、
a>0の場合には、x>0の範囲の定義域だけの関数
S(x)=0, (x>0)
だけが得られます。この定義域でs(x)=0は連続関数です。
a≦b<0の場合には、x<0の範囲の定義域だけの関数
S(x)=0, (x<0)
だけが得られます。この定義域でS(x)=0は連続関数です。
a=0の場合には、S(x)が計算できません。
この積分の式で定義される(定義可能な)不定積分:
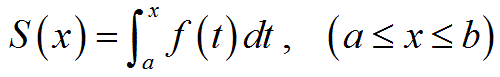
は必ず連続な関数です。
しかも、この不定積分には、定数C1もC2もあらわれません。
そのため、この不定積分は、原始関数F(x)とは異なります。
微分積分学の基本定理によって、
原始関数F(x)を使って被積分関数f(x)の定積分が計算できる事が完全に保証されているのは、f(x)が、その積分区間で連続なときだけです。
それ以外の場合には、その計算の答えが間違っていることがある、という事を認識しなければなりません。
(なお、微分積分学の基本定理が積分可能性を完全に保証する条件であるf(x)が積分区間で連続でなければならないという条件は、緩める事ができ、f(x)の原始関数F(x)が積分区間で連続であるだけで良いということが分かっています。これは、後で詳しく説明します。
(誤解された原始関数の差で計算するから間違えるのであって、不定積分(必ず連続関数になる)の差で定積分を計算するならば、この様な間違いは起きません。不定積分(いつも連続関数)の差で定積分を求めたと書く答案が一番正しい答案だと思います。)
微分積分学の基本定理の登場により我々に注意が喚起されたメッセージは、
『関数f(x)の積分を計算しようとする場合には、その積分区間における関数の性質(連続である等)を調べなければならない』
というメッセージです。
原始関数を用いて定積分を計算する演算の際に、その定積分の積分区間における関数の性質を調べる事を欠かしてはならない、というメッセージです。
この大切なメッセージは、日本の高校の積分の授業では、教えられていません。
そして、高校で習う、
「原始関数F(x)を使って、以下の計算で定積分する。」
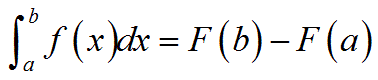
に従って計算すると、
不連続な誤解された原始関数を使った計算では、先の例の様に間違った答えになります。

上の図のマイナス無限大の面積が、
以下で説明するように、全く違う間違った答えになります。
F(x)=1/xをxで微分したら上図の被積分関数f(x)=-1/x2になるので、
関数f(x)=-1/x2の誤解された原始関数がF(x)=1/xです。
そして、誤解された原始関数F(x)を使って:
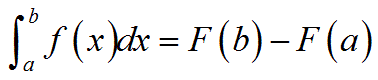
の式を使って、
f(x)が不連続になるx=0を含めた、xが-1から1までの区間の定積分を計算すると、
F(1)-F(-1)=1-(-1)=2
と 計算されます。
この答えは、明らかに間違いです。
(誤解された原始関数の差で計算するから間違えるのであって、不定積分(必ず連続関数になる)の差で定積分を計算するならば、この様な間違いは起きません)
【微分積分を学ぶとき注意すべき点】
また、微分を理解するためには、以下の事も整理して学ぶ必要があると考えます。
変数xで表される2つの関数があって、
変数xのある値xにおける、2つの関数のxによる微分係数が、以下の式であらわされて等しい場合に:

この関数を他の変数tで微分した場合に、

が成り立つと普通は考えますが、それが成り立たない場合もあります。
それが成り立つ場合と成り立たない場合を区別する条件は、「合成関数の微分の公式」を学ぶことで理解されますが、それが高校生には教えられていません。
変数xを変数t≡(x-1)に置き換えて、その変数で微分してみるといった変数変換は頻繁に行われます。その変数変換の中にはやってはいけない変数変換があると言われたら一歩も計算を進めることができなくなります。
その「やって良い変数変換」とは何なのかが分かるようになるまでしっかり勉強して下さい。
高校教科書ではそれは教えていません。
微分積分の勉強は、高校教科書からでは無く、自分で良い微分積分の参考書(大学1年生向けの参考書が良い)を探して、勉強するようにしてください。
例えば、「やさしく学べる微分積分」(石村園子) ¥2000円 が、内容がわかり易くて良いと思います。
その36ページから45ページまで勉強すれば、「合成関数の微分の公式」まで勉強でき、「やって良い変数変換」が何なのかが分かるまでの勉強ができると思います。
[室蘭工業大学 山口 格] “論証"・論証"とやかましくいっておきながら,微積のところへ来ると,とたんにいいかげんな議論でごまかしている。一ーまた高校ではごまかさざるを得ないだろう。高校数学の目的は生徒のあたまを混乱させることにあるのだろうか。
現在の高等学校の教科書は,積分の概念の説明を回避している。
1997年からは、日本の高校の数学IIで面積が無定義に用いられという、数学センスを否定する蛮行が行なわれた。そして、関数f(x)のグラフとx軸で囲まれる領域の面積を,x方向で微分するともとの関数f(x)になり、面積の微分がf(x)となるという本末転倒なことを教えるようになった。
このような、数学センスに反する無価値な情報をおぼえることを強制された場合、それを覚えることを拒否して良いと考えます。
一つの選択としては、理系に進むのを止めて文系に進むことがあります。
しかし、数学が好きな学生には、それはできない、と考えます。
その学生のために、以下の様に微分積分を学ぶことを推薦します。
(微分積分の学び方)
ヨーロッパやアメリカでは、「高校で微分積分を教えるのは、直感にうったえる内容に限られ、正確な微分積分を教えられない」という理由で、微分積分は大学生に教える科目になっています。
日本の大学でも、その欧米の教育に合わせて、初めて学ぶ者に分かるように微分積分を改めて教育しているようです。
大学で使う微分積分の参考書は、高校で教える微分積分の知識を全く知らない学生に理解できるように書かれています。
しかも、大学生向けの微分積分の参考書の方が、日本の高校生向けの微分積分の参考書よりやさしく分かり易い。
高校の微分積分を勉強するなら、先ず、大学生向けの微分積分の参考書を読むことを推薦します。高校の微分・積分の教科書は分かりにくいだけで無く、間違いも含まれています。読まない方が良いのではないかと考えます。
微分については、大学生向けの参考書の
「微分積分学入門」(横田 壽)
を読んでみることをお勧めします。
(注:横田教授が芝浦工業大学を退官したため、この教科書を無料で掲載していたWebページが無くなりました。この本は書店で購入できます。)
(しかし、同じ著者の書いた高校生向けの参考書「確実に身につく微分積分(2012年)」の1版は、内容が劣化しているのでお勧めできません。大学生向けの本物の知識の参考書「微分積分学入門(2004年)」を読んでください。)
その他に、高校2年生が勉強するのに適切な、書店で購入できる微分積分の参考書は:
「やさしく学べる微分積分」(石村園子) ¥2000円
が内容がわかり易くて良いと思います。
「微分積分学入門」(横田 壽)の読み方は、 66ページから始まる2章「微分法」の以前のページは斜め読みして、何が書いてあるらしいかを漠然と把握しておいて、
66ページ以降の2章「微分法」をお勧めします。
読んでいるうちに知らない関数や概念が出てきたら、66ページ以前に書いてありますので、探して、その部分を読んで理解するように勉強してください。
積分については,ここをクリックした先のpdfファイルにある原教授の以下のコメントが大切です。
---(原教授のコメント開始)---------
積分については高校でも習ってはいるが,その基礎を突き詰めていくといろいろと困ったことがでてくる.
特に 「積分は微分の逆演算」として定義すると,「ある関数 f の積分を求めよ」という問題や「この関数の積分は定義でき るか?」という問題でハタと困ってしまう.
(微分して f になるような関数がわからない場合,高校までの知識ではお手上げだ.)
この節では高校までの知識はいったん忘れて,「積分とは何か」「積分をどのように定義すべきか」か ら話を始める.
4.1 積分(定積分)の定義
ということで,まずやるべきは「与えられた関数f(x) に対して,その積分を定義すること」である.
これから見ていくように,かなり広いクラスの関数に対してその積分(定積分)を定義することができる.
定積分を通して不定積分も定義できるので,高校までの知識とのつながりがつくことになる.
・・・
積分の最も素朴な定義はこれから紹介する「リーマン和」に基づくもので、、、
---(原教授のコメントおわり)------
「微分積分学入門」(横田 壽)は、積分の説明もわかり易いのでお勧めですが、先ずは124ページのリーマン積分を読んでから、次に、その前のページに書かれている積分の説明を読んで欲しい。
(積分の計算の基本)
以下のグラフのように、面積を分割して、分割した要素の総計を求めてグラフの面積を計算する手法が「定積分」です。
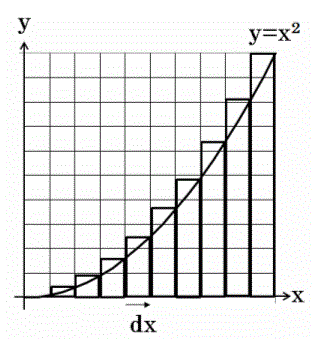
この計算のための法則性を整理して覚えることが「積分」を勉強するということです。
(「リーマン積分可能」の定義)
「微分積分学入門」(横田 壽)の124ページから125ページに「リーマン積分可能」の定義が書いてあります:
ここではドイツの数学者G.F.B. Riemann (1826-1917) によって示されたRiemann 積分につ いて学んでいきます.リーマン積分による「積分可能」の定義は、全ての種類の「積分可能」の定義の基礎になっています。
f(x) は閉区間[a, b] で定義されているとします.この閉区間[a, b] を次のような点xi(i = 1, 2, . . . , n) でn 個の小区間に分割します.
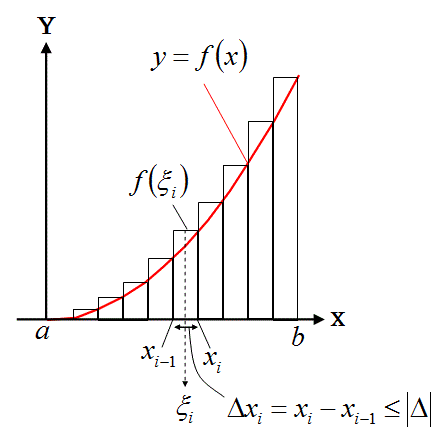
(a = x0 < x1 < x2 < · · · < xi < · · · < xn = b)
この分割をΔ で表わし, Δxi = xi − xi−1 (i = 1, 2, . . . , n) のうちで最も大きい値を|Δ| で 表わします.
いま,それぞれの小区間[xi−1, xi] のなかに任意の点ξi をとり,Riemann 和 (Riemann sum) とよばれる次の和を考えます.
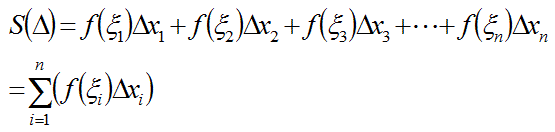
このとき、
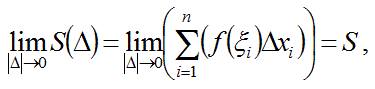
となる実数S が存在するならば,このS をf(x) の定積分(definite integral) といい, f(x) は閉区間[a, b] で積分可能(integrable) であるといいます.また,このS を次のように表わします.
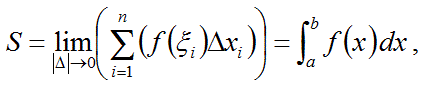
つまり関数f(x) が閉区間[a, b] で積分可能であるということは,分割の仕方および点ξi(i = 1, 2, . . . , n) のとり方に関係なく、各点の関数値の和が一通りに定まるということです.
この定義に従い、関数の積分可能性を以下の様にして調べることができます。
先ず小さな閉区間[a, b] を定めて、
その閉区間の小区間への分割の仕方および点ξi(i = 1, 2, . . . , n) のとり方に関係なく、各点の関数値の和が一通りに定まる(積分可能)か否かを調べることができます。
(積分可能な例1)
以下の図の関数f(x)のグラフを考えます。以下のグラフはX=0の点とX=2の点で不連続なので、微分積分学の基本定理により積分可能であると保証されているわけではありません。
そういう関数ですが、リーマン積分という厳密な積分の定義を使って考える事で、この関数が積分可能か否かが判別できます。

この関数は、x=0の点での極限とx=2の点での極限が存在しません。
x=0の点とx=2の点で関数は不連続であり、また、極限も存在しませんが、
-1≦x≦3
の区間を細分した各小区間での関数の値の和が一通りに定まるので、その連続で無い点を中間に持つ区間でも積分可能です。
この関数f(x)を積分して、以下の図の関数F(x)を求めることができます。
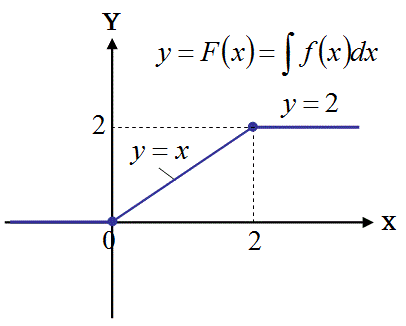
この関数F(x)を微分して下図のグラフの関数を求めます。
x=0とx=2の点では、微分係数が存在しないので、その点では微分できません。
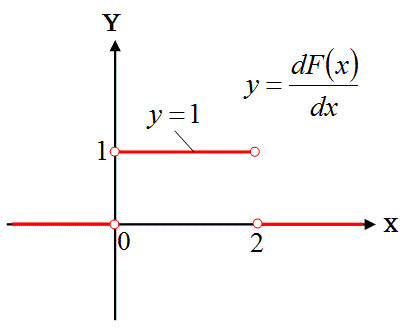
この(dF(x)/dx)のグラフは、x=0とx=2で関数値が存在しないという点で、その点では関数f(x)と異なるグラフになるという特徴があります。
(F(x)は関数f(x)の不定積分)
しかし、関数F(x)をx≠0とx≠2となる変数xの範囲:
0<x<2
を定義域にした関数にすれば、その定義域で、関数F(x)の微分が関数f(x)になる。
よって、その定義域:
0<x<2
で定義された関数f(x)の原始関数が、その定義域:
0<x<2
で定義された関数F(x)です。
この微分結果のグラフを再度積分したらどうなるでしょうか。
その積分結果は、再び同じ関数F(x)が得られると考えます。
x=0の点とX=2の点の有無で異なる2つのグラフを積分したら、同じ不定積分F(x)が得られました。
そのため、関数f(x)に積分結果の関数F(x)を対応させる写像変換は、
2個以上の関数f(x)に1つの関数F(x)を対応させる、
複数対1の写像であると考えられます。
(注意)
ちなみに、微分不可能な点がある関数F(x)は原始関数では無いというのは、原始関数を必ず微分可能な関数とした真の原始関数の定義に基づく考えです。
上の例の、x=0の点とx=2の点で折れ曲がって微分不可能な点を持つ不定積分F(x)は、関数f(x)からx=0の点とx=2の点を除外した関数が微分の結果になる不定積分です。この不定積分の方が原始関数より広い範囲の関数を扱え実用的です。
(厳密に考える)
ここで、厳密に考えると:
原始関数F(x)を微分すると、x≠0とx≠2の範囲でのみ定義されている関数が得られました。
f(x)の不定積分F(x)は、その得られた関数の原始関数です。
しかし、x=0で、f(0)=1であり、x=2で、f(2)=1である関数f(x)は、関数F(x)の微分によっては、x=0での点とx=2での点が得られません。
厳密に言うと、このf(x)の不定積分F(x)は、f(x)の原始関数F(x)ではありません。
しかし、f(x)を定積分するために利用する関数としては、この不定積分F(x)で十分です。
(積分可能性が保証される条件とは)
上図の場合では、関数f(x)が不連続な点があっても積分できました。これは、以下の条件を満足したからです。
関数f(x)が積分可能な条件は、関数f(x)の積分区間内でf(x)の原始関数F(x)が連続な場合だけです。
関数f(x)を積分する区間は、原始関数F(x)が連続な範囲の、例えば、
a≦x≦b
という区間で積分が可能です。
例えば、以下の図の、x=0で不連続な関数f(x)は、その連続で無い点以外の変数xの範囲内で連続で、その原始関数F(x)も連続です。その区間で、この関数が積分可能です。

このグラフの関数の事例では、x=0の点では関数f(x)の値が-∞になり、また、広義積分によって原始関数F(x)を計算しても、その原始関数F(x)もx=0で不連続になるので、x=0を含む区間で積分することはできません。
(積分できない例を示す図)

関数を、上図の区間で積分したら、マイナスの無限大になるので、積分が不可能ですので、
例えば、上図の関数をー1から1までの区間で積分する事も不可能です。
関数f(x)=-1/x2を、連続で無い点x=0で積分していけない理由は、
この関数f(x)に対しては原始関数F(x)=1/xが求められ、
その原始関数F(x)が、f(x)の積分範囲内のx=0で、連続で無い点を持ちました。
このように、
関数f(x)の原始関数F(x)が得られても、
f(x)の積分範囲内にF(x)が連続で無い点を持つ場合は、
その積分範囲では関数f(x)の定積分を:F(b)-F(a)
で計算してはいけないと認識する必要があります。
(ハッキリ言うと、不連続な誤解された原始関数の差では計算せず、不定積分(必ず連続関数である)の差で定積分を計算すべきです)
一方、
関数f(x)の積分範囲内では不定積分F(x)が連続であったなら、
その積分範囲では関数f(x)の定積分を:
F(b)-F(a)
で計算して良いです。
これについては、数学者の藤原松三郎の「微分積分学 第1巻」が、
不連続関数f(x)の積分を広義積分と呼び、
その積分において、関数f(x)の積分範囲
a≦x≦b
内で連続な不定積分(その積分範囲内に微分不可能な点があっても良い)F(x)が得られたら、
(1)それは、不連続関数f(x)が積分可能である証拠であり、
(2)以下の計算で定積分を計算して良い事が書いてあります。
F(b)-F(a)
よって、
不連続な関数f(x)に対して、
不定積分F(x)が見つかり、その不定積分がf(x)の定積分の連結区間内で連続ならば(その区間外に連続で無い点が有っても良い)、
その不定積分F(x)を使ってf(x)の定積分を計算して良いです。
また、小寺平治・著「はじめての微分積分15講」(2,200円)の103ページにも、このことが書いてあります。
(誤解された原始関数の差で計算するから間違えるのであって、不定積分(必ず連続関数になる)の差で定積分を計算するならば、間違いは起きません。不定積分(いつも連続関数)の差で定積分を求めたと書く答案が一番正しい答案だと思います。)
積分可能である事が完全に保証される条件(関数f(x)が積分区間内で連続な関数でなければならない)から外れている場合にあえて積分する例を、更に考えてみます。
以下の例では、被積分関数f(x)がある点で連続な連続関数である場合と、その関数の1点の関数値が存在しない(あるいは0等の値になる、その点では不連続な関数である)場合とが区別されずに、その範囲を積分した結果が同じ値に計算されます。
不連続な関数f(x)を:
変数xが整数の点では関数値が存在せず、
変数xが整数以外の点では値が1、
である不連続な関数とします。

(上図において、x=整数の連続で無い点のxの値に対して、そのxの値における極限の値をf(x)の値に置き換えてf(x)=1とすれば関数が、その点でも連続な連続関数になります。そういう連続で無い点のことを、「除去可能な不連続点」と呼びます。)
この点で連続で無い関数 f(x)のグラフを積分したら、
連続な関数 F(x)=xが得られます。
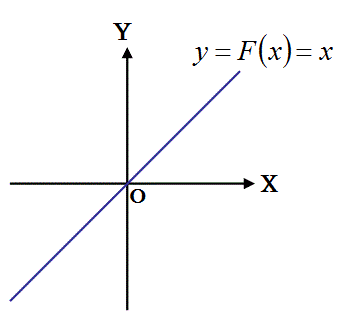
この連続関数F(x)=xを微分したら、
連続関数であるy=1が得られます。

(関数f(x)の不定積分F(x)について)
こうして、f(x)の不定積分F(x)を微分すると大部分のxではf(x)には戻りますが、戻らない点もありました。この不定積分F(x)は、上図の関数y=1の原始関数です。
このように、微分積分学では、あらゆる関数に微分積分を行う理論を作ろうとすると、いろいろな難しい問題があることがわかりました。
積分前の関数f(x)と、微分前の関数F(x)との、変数xの一部の定義域での微分積分のあり得る関係が以下の図であらわせます。

(上図で、関数f2(x)は、除去可能な不連続点を除去した関数です。関数F(x)は、関数F(x)の連続で無い点を除いた変数xの範囲でf(x)の原始関数であるとともに、f2(x)の原始関数でもあります)
上図の、f(x3)とF(x3)の関数のセットの例:
以下で定義する関数のセットでは、f(x)にx=x3で除去不可能な不連続点があって、積分した結果のF(x)がその連続で無い点の位置x3でも変数xで微分可能で、F(x)を微分すると再び連続で無い点を持つf(x)が得られます。
(F(x)の定義)
x≠0の場合:
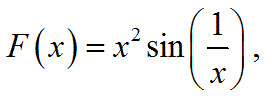
x=0の場合: F(0)=0,
(導関数f(x))
この関数F(x)はx≠0の場合も、x=0の場合も、微分可能で、
その導関数f(x)は、以下の式であらわせます。
x≠0の場合の微分:
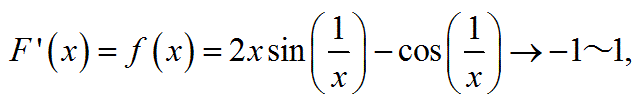
になり、xが0に近づくとー1と1の間を振動します。
この導関数が含むcos(1/x)の関数が以下のグラフであらわす形の関数になるからです。
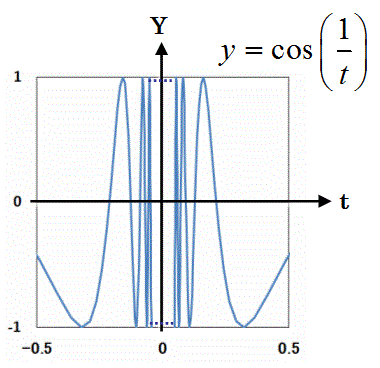
X=0の場合にも、F(x)は微分可能で:

というように、0になります。
そのため、この導関数f(x)は、x=0で連続ではありませんが、F(x)を微分することで得られます。
この導関数f(x)は積分可能であり、積分するとF(x)になります。
このように、関数の不連続点がらみで、関数f(x)とF(x)の間に難しい関係があることが分かりました。
微分積分の有り得る関係の図には、関数F(x)が変数xの定義域内のある連結区間内で微分可能の場合には、その微分結果の導関数f(x)が、その連結区間で必ず積分可能になり、その積分結果がF(x)になるパターンがあります。そういう連結区間を定義域にした関数F(x)とf(x)だけに限って微分積分をするならば、難しい問題が生じず、計算が簡単になります。
微分積分学で、難しい問題が生じない関数の範囲を把握して、その範囲内で微分積分の計算をすることで、応用上で微分積分を使い易くできます。
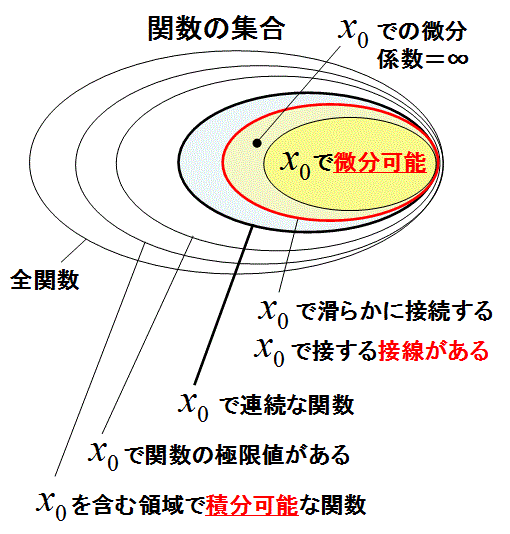
そのため、使い易い関数として、変数xの定義域内の所定の範囲内では、関数の極限が存在し、かつ、関数が連続な「連続関数」 を主に扱う対象にします。また、「微分可能性」で関数の変数xの定義域内の所定の範囲を制限して、微分積分を行う所定の範囲を制限します。その関数の集合において、その制限条件を満足する(変数xの)範囲内で成り立つ法則を把握して、種々の公式を導き出して使うことで微分積分学を最大限に応用できるようになります。
微分積分学は、変数xの所定の連結区間で、微分可能な関数F(x)と積分可能な関数f(x)を定義して、その種の関数の間で微分したり積分をします。「微分可能」と「積分可能」という制限条件を定め、その制限条件を満足する関数を扱うのが微分積分学だと認識することがとても大切です。
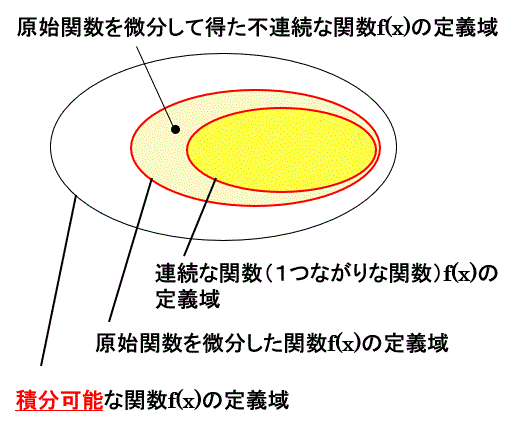
《下図に各種の関数の集合の包含関係をまとめた》
リンク:
高校数学の目次