先ず、閉区間で連続な関数の最大値と最小値の定理を高校生が理解できないようにする高校数学で、学生に間違いを教えている間違いを正す必要があります。
数学者の小平邦彦「[軽装版]解析入門Ⅰ」では、微分積分を使いものになる道具にするため、数学の定理で連続関数を使うときに必ず使う形に整合させて連続関数を定義しています。すなわち、連続関数という言葉を、連結区間で1つながりに連続する関数と定義しています。
また、使いものにならなくなっている「不連続点」と言われている言葉を使わず、微分積分の概念の理解のために役立つ言葉で、連続点以外の点をあらわす「連続で無い点」という言葉を使っています。そのため、当ブログでも、小平邦彦「[軽装版]解析入門Ⅰ」に従って、「不連続点」という言葉は使わず、「連続で無い点」という言葉を使います。
(不連続点の当初の定義も、連続で無い点の定義と同じでした。藤原松三郎の「微分積分学 第1巻」によると、「f(x)がx=ξで連続でない場合に、x=ξをf(x)の不連続点という。」と定義されていました。)
(1)第1の定義の連続関数:
(連結した)開放された区間(a<x<b)で連続な関数f(x)。その開放区間内のどの点でも完全に連続な関数。
すなわち、両端が開放された連結区間で1つながりに連続する関数。
(2)第2の定義の連続関数:
(連結した)閉区間( a≦x≦b)で連続な関数。a<x<bとなるどの点でもf(x)が完全に連続。x=aとx=bとの端点では、片側連続である関数f(x)。
すなわち、端点を持つ連結区間で1つながりに連続する関数。
との2通りの定義があります。
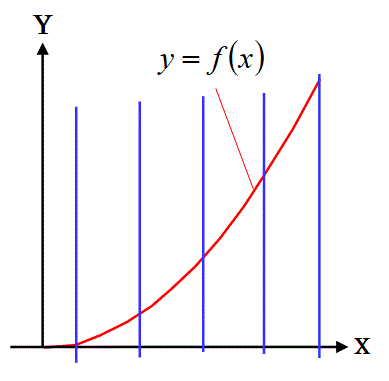
上図の関数f(x)は、X=0とX=2で不連続ですが、
その0≦x≦2の区間内の部分の関数f(x)は、
閉区間0≦x≦2で定義された連続関数です(第2の定義の連続関数)。
また、「区間」という数学用語は、実数の集合として定義されている用語である事に注意が必要です。
a≦x≦bを満足するxの区間という表現は、a≦x≦bの範囲内の全ての実数xという意味です。
-∞<x<∞という区間もあります。
区間はxの値の範囲を限定するためのa≦x≦bという式とは意味が異なることに注意する必要があります。
(A)「0≦x≦2の区間の変数xで定義された関数f(x)がその区間の各点で連続であるとき,f(x)は連続関数である」という文では、
f(x)は、0≦x≦2の区間で1つながりに連続した関数f(x)として定義されます。
一方で、
(B)「変数xの0≦x≦2の範囲内の値で関数f(x)が定義されていて、その関数f(x)が定義域の各点で連続であるとき,f(x)は誤解された連続関数である」という文では、f(x)は、例えば、
0<x<1で f(x)=0, この定義域内の各点で連続。
1<x<2で f(x)=1, この定義域内の各点で連続。
結局、0≦x≦2の範囲内の全ての定義域の各点で連続な誤解された連続関数f(x)として定義されます。
この例の様に、「区間」という用語は変数xの集合をあらわす用語であって、変数xの範囲をあらわす用語では無いことに注意する必要があります。
区間a≦x≦bが命題の中に記載されている場合は、その範囲内の全ての実数xについて命題を検討する必要があります。被積分関数f(x)が定義されていない変数xの点があっても、その点も、その命題が検討されるべき点の1つです。
【連続関数の誤った定義が問題を起こしている】
高校の教科書では「定義域」という言葉を使って、
「関数 f(x) が、定義域のすべての x の値で連続であるとき、 f(x) は連続関数である、という。」
と書かれていると思います。
しかし、中学生のときから教わって来た「定義域」という言葉の定義が、高校以上の数学では、所定の区間を指すだけではない、様々な場合を含むように変わりました。
変数が自然数だけの関数の定義域は自然数だけといったぐあいです。
定義域が自然数だけの関数の連続性を考えるのは、とても不自然です。
なお、y=1/xは、x=0で不連続ですが、
x=0での関数値が無い、すなわち、x=0は定義域に含まれない。
そして、x=0以外の、全ての定義域の点で連続なので「連続関数」と呼ばれています。
しかし、定義域という言葉は、関数f(x)の値が存在する変数xの値の集合の事であって、その集合に含まれないxの値であっても、変数xの数直線上の値は存在します。
(定義域のあるxの値に対しf(x)の値が存在しないと関数を決めるだけで、どの変数xの値も定義域から排除できます)
xの値の所定区間において、x=0の値に対してf(x)の値が無いので、x=0において関数f(x)は連続ではありません。そのため、f(x)を「連続関数」と呼ぶには違和感があります。
(注意)
「不連続点」である条件は、その不連続な値で関数値f(x)がある事と決められているため、上の例のx=0のように関数値f(0)が存在しない点は不連続点とは呼ばれません。
不連続点という言葉では、変数xの所定区間でf(x)が存在しないためf(x)が連続で無い事実を表現できなくなっています。
そのため、当ブログでは、上の例のx=0の点は、連続で無い点と呼び、「不連続点」という不完全な言葉は使わない事にします。
【高校数学での連続関数の定義の間違い】
高校数学で連続関数を定義域で連続な関数として定義する事の重要な第1の欠陥は、連続関数という言葉を使ってあらわされている全ての定理は、それと異なる連続関数の定義を前提にしている定理であるから、それらの定理の全てを無視すること、更に、その無視された定理を少しでも使う全ての定理を無視することを強いる事だからです。
第2の欠陥は、連続関数を定義域で連続な関数として定義する事ができても、それによって定義された「連続関数」は、何ら数学的に特徴的な関数を定義したことになっていない、数学の研究には何も役立たない無意味な定義だという欠陥があります。
閉区間( a≦x≦b)で連続な関数f(x)は、
その区間内で有限の値の最大値と最小値を持つ。
(ここまでが定理)
この定理は、誤った連続関数の定義と異なる、正しい連続関数の定義を前提にした定理です。そのため、この定理は、高校数学では無視することが強いられています。
高校数学では、
y=1/xは、x=0以外の、全ての定義域の点で連続なので「連続関数」と呼ばれています。
また、高校数学では、閉区間( a≦x≦b)とは、変数xの値の範囲を限定する式のことであるという間違いが教えられています。
その誤った知識に基づくと、
【閉区間で連続な関数の最大値・最小値の定理】とは、
変数xの範囲( a≦x≦b)内に関数が連続である定義域を持つ連続関数f(x)は、
その範囲( a≦x≦b)内で有限の値の最大値と最小値を持つ。
(ここまでが定理)
という定理と解釈されます。
この「定理」には以下の反例があります。
関数f(x)=1/xは、
変数xの範囲
-1≦x≦1
内に定義域(ただしx≠0という定義域)が存在し、
-1≦x≦1
内で定義されているどの点でも連続なので、
連続関数です。しかし、この連続関数f(x)は、
x→0の近くで∞と-∞に発散するので、
有限の値の最大値と最小値を持たない。
(反例おわり)
しかし、この定理の基礎となっている連続関数の定義が高校数学の定義とは違うので、これは定理の反例にはなっていません。
以下で、正しい連続関数の定義と、区間という数学用語の正しい定義に基づき、この最大値・最小値の定理を証明します。
閉区間( a≦x≦b)で連続な関数f(x)は、
その区間内で最大値と最小値を持つ。
(ここまでが定理)
この定理を正しい連続関数の定義に基づき、以下の様に言い換える事ができます。
(最大値・最小値の定理の言い換え)
連結区間( a≦x≦b)の範囲内の全ての実数xに対して有限の関数値f(x)が存在する。そして、その範囲内の全ての点で関数f(x)が1つながりに連続な連続関数であるものとする。
その場合は、その範囲内( a≦x≦b)での関数の値f(x)の全てが、有限な値の最大値と最小値との間にある。
(定理の言い換えおわり)
この定理は、明らかなように見えますが、そう見えるのは、連続関数というものを自分の主観で限定して考えているからです。
「下図の様に、連続する線を曲げて上下に振動させるグラフを作る。
そのグラフの最大の振幅のx座標の半分の値のx座標の点を、先のグラフ最大の振幅の2倍の振幅に変形させたグラフを作る。
この作業を無限に繰り返して連続なグラフを変形させていったグラフの関数f(x)を作ったらどうか?」
「連続な関数のグラフを切らずに作ったグラフの関数だからf(x)は連続関数では無いのか?そして、最大値Mが無限に大きいグラフが作れるのではないか?」
というように問われたら、
「 いや、そうなったら、それは、もはや、その無限にグラフを細かくしている点x=0で不連続になり、連続関数で無くなります。」(事実はこの通りですが)
と即答できるでしょうか。
こういう問題に論理的に(数学的に)返答できるようにするため、連続が、以下の様に数学的に定義されています。
【第1の定義の連続】
「微分積分学入門」(横田 壽)の39ページ近くに、連続の第1の定義が書いてあります。
極限を求める点が連続で無い点であっても定義される関数の極限、
を考えるときには、
x0 での関数f(x)の値f(x0)が定義されている必要はありませんでした。
また,x0 での関数f(x)の値 f(x0) が定義されていても、その値 f(x0) がx0 での極限値
と一致する必要もありませんでした。
そのように無制限な関数の条件に、新たに、
極限値とそこでの関数の値が等しいという条件を加えてみます。
そうすることは,以下で説明するように、
関数がある点で連続である
という条件を加えるという意味を持ちます.
【定義1.4 (連続) 】
関数f(x) は少なくとも、微小な連結区間
x0 − δ<x<x0 + δ
の全ての点で定義されている.
(ここで、δは小さな正の実数)
が成り立つとき, f(x) はx = x0 で連続(continuous) であるという.
-----(定義の言い換え)----
この定義をハッキリ把握するために、想像力を膨らませて、この定義を、以下の様に噛み砕いて自分の言葉で言い換えて定義を覚えてください。
(なお、この定義をかみ砕いて考える考え方が、小平邦彦「[軽装版]解析入門Ⅰ」の80ページから81ページに詳しく書いてあります。)
(0)
この、関数の1点での連続の定義は、関数の1点の近傍の幅を持った区間で連続を判定しています。
すなわち、関数の連続を確認する点x=x0 については、その点の座標の周りに広がりを持つ区間の、少なくとも、x0 − δ<x<x0 +δ
(ここで、δは小さな正の実数)
という連結区間の全ての実数値xで関数f(x)が定義されていることが大前提です。
「区間」と言う場合は、それは1つの連結区間であって、その区間内の全ての実数が関数の定義域である事を意味します。
(1)
次に、
x0に近い(値x0も含む実数)xを考える。
(2)
x0から、正の値δの範囲内でずれる、x0も含む全ての実数xについてf(x)を考える。
この定義における「全ての実数x」の意味は、例えば関数の変数xの定義域による変数xの値の制限も無視して、その制限に制約されずにx0から、正の値δの範囲内でずれる値の実数変数xは全て考慮することを意味します。
(3)
その全てのf(x)の値のバラツキの誤差を求める。
その誤差<εとする小さな正の値εでバラツキの範囲を定める。
すなわち、どの実数x(ただし、x=x0の場合も含む)の値の関数値f(x)についても、
-ε< (f(x)-f(x0))<ε
となる正の値εを定める。
(4)
xの値のx0からずれる範囲を定める正の値δを十分小さくすれば、
その範囲内の全ての実数値のx(値x0も含む)によるf(x)の値のバラツキが小さくなり、バラツキの範囲の値 ε がいくらでも小さくできるならば;
f(x)はx=x0 で極限値を持ち、かつ、その極限値がf(x0)に等しい。
その場合に、
関数f(x)は、
x=x0 で連続である。
すなわち、
が成り立つ場合に、関数f(x)はx=x0 で連続になります(第1の定義の連続)。
言い換えると、
「点x0でf(x)が連続である定義は、
どんなに小さい正の値εに対しても、
十分小さい正の値δを使ってxの区間を、
x0 − δ<x<x0 +δ (x=x0となる場合も含む)
に限定すれば、どのxの値でも、
-ε< (f(x)-f(x0))<ε
が成り立つようにできる事である。」
----(定義の言い換えおわり)-----------
(注意1)このε-δ論法による連続の第1の定義は、
xの区間の x0 − δ<x<x0 +δ を使っていますので、その区間の全ての実数についてf(x)の値が存在する(定義されている)事を条件にしています。そのため、以下の例の様に関数値f(x)が区間で定義されていない場合は、連続であるとは定義しません。
x=0,1,2だけで定義された関数f(x)の例:
f(0)=10,
f(1)=11,
f(2)=12,
この関数f(x)は、
どんなに小さい正の値εに対しても、
正の値δ=0.5を使ってxの範囲(区間では無い)を、
1− δ<x<1 +δ
に限定すれば、
その範囲内のf(x)の定義域のxの値は、x=1のみになる。
その全てのxの値(x=1だけですが)に対して、
-ε< (f(x)-11)<ε
が成り立つようにできます。
ε=1/10000という小さなεの場合でも上の式が成り立ちます。対象となるxはx=1しか無いからです。
しかし、そうであっても、f(x)はx=1で連続ではありません。
連続の定義では、区間
1− δ<x<1 +δ
内の全て実数に対して、f(x)の値が存在する事を要請しているが、関数f(x)はその条件を満足しないからです。
(注意2)ここで、ε-δ論法が出て来ましたが、ε-δ論法というものは、εとδを使った極限の表現の手段であって、そのε-δ論法を使った「連続」の定義は、上の形の第1の連続の定義に限られません。
以下で説明する片側連続についても、第1の連続の定義とは形を変えた別のε-δ論法によって片側連続が定義されます。
【第2の定義の連続】
閉区間(a≦x≦b)で定義された、第2の定義の連続関数f(x)は、多くの場面で使われます。
閉区間(a≦x≦b)で連続な連続関数f(x)と呼ばれますが、
その定義域の端点では、片側連続であり、両側からは連続していなくても閉区間で連続と定義しますので要注意です。
上図の関数f(x)は、X=0とX=2で不連続ですが、
その0≦x≦2の区間内の部分は、
「区間0≦x≦2で定義された関数f(x)が区間0≦x≦2で連続な連続関数である」
と言います(第2の定義の連続関数)。
(第2の定義の連続関数の端点での連続の定義)
(1)
関数f(x)が、閉区間a≦x≦bで定義され、a<x<bの点でf(x)が連続であって、
(2)
閉区間の端点bでは:
x → b− 0 またはx → b− と表わす左側極限値f(b-)がf(b)である左連続によって連続です。
すなわち、端点bでのグラフの点(b,f(b))が左側極限の点(b-,f(b-))と連続している(片側連続性)。
左連続の定義は、ε-δ論法によって以下の様に表現することができます。
どんなに小さい正の値εに対しても、
十分小さい正の値δを使ってxの区間を、
b-δ<x≦b (x=bとなる場合も含む)
に限定すれば、どのxの値でも、
-ε< (f(x)-f(b))<ε
が成り立つようにできるならば閉区間の端点x=bで連続である。
(3)
閉区間の端点aでは:
x → a+ 0 またはx → a+と表わす右側極限値f(a+)がf(a)である右連続によって連続です。
すなわち、端点aでのグラフの点(a,f(a))が右側極限の点(a+,f(a+))と連続している(片側連続性)。
右連続の定義は、ε-δ論法によって以下の様に表現することができます。
どんなに小さい正の値εに対しても、
十分小さい正の値δを使ってxの区間を、
a≦x<a+δ (x=aとなる場合も含む)
に限定すれば、どのxの値でも、
-ε< (f(x)-f(a))<ε
が成り立つようにできるならば閉区間の端点x=aで連続である。
そういうふうに、閉区間(a≦x≦b)で定義された関数f(x)は、その閉区間の端点a,b間で連続な関数f(x)であると定義されています。
関数f(x)が右側極限や左側極限で区間の端点に片側連続性で連続につながっているので、そういう表現をする理由になっています。
-----第2の定義の連続関数の説明おわり-----------
最大値・最小値の定理は、最大値がある事を示せば、同様にして最小値がある事も示せるので、最大値がある事を証明するだけで十分である。
【最大値の定理の証明】最大値の定理の対偶の定理:
閉領域内で関数値f(x)が有限の値Mに制限されない場合には、その閉領域内の少なくとも1つの点の座標xの関数値f(x)が無限大に発散し、その点xでは関数が不連続になる事を、以下の様にして証明することで、最大値の定理が証明できます。
上図の閉領域で、関数値f(x)が有限の値Mに制限されないならば、その閉領域を、以下の様に半分に分割した2つの閉領域(ただし、その分割点は両側の閉領域に重複して含ませる)の少なくともどちらかの閉領域で、関数値f(x)が有限の値Mに制限されない。
そして、その、関数値f(x)が有限の値Mに制限されない閉領域を、更に半分に分割した2つの閉領域の少なくともどちらかの閉領域で、関数値f(x)が有限の値Mに制限されない。
そして、その、関数値f(x)が有限の値Mに制限されない閉領域を、更に更に半分に分割した2つの閉領域の少なくともどちらかの閉領域で、関数値f(x)が有限の値Mに制限されない。
この操作を無限に繰り返すと、
関数値f(x)が有限の値Mに制限されない領域が無限に小さくなっていきます。
その場合に、その領域内の点のx座標が、極限値xgに収束する(ここをクリックした先の定理18)。
その極限値xgの近くでは、
どんなに小さなδを選んでも、
xg − δ<x<xg +δ (ただし、x=xgの場合を含む)
を満足する実数値xの領域内に、
無限に小さな領域ではあるが、関数値f(x)が有限の値Mに制限されない領域が含まれます。
そのため、その領域の実数xのなかに、
関数f(x)の値を有限の値Mに制限しない無限に大きく発散させる点のxがあります。
その点のxでは、
小さなεを選んで、ある有限の値 lim に関して、
-ε< (f(x)-lim)<ε
とすることができません。
それは、
x→xg (ただし、x≠xg)
でのf(x)の極限値が無いか、
又は、
(x≠xgでの)極限値(それは有限の値Mに制限される)があっても、
x=xgの場合のf(x)が有限の値Mに制限されず、
すなわち、
f(xg)は、
(x≠xgでの)x→xgでのf(x)の極限値とは異なる、
ということを意味します。
それは、
x=xgでf(x)が不連続である事を意味します。
よって、
閉領域で関数値f(x)が有限の値Mに制限されない場合には、
その閉領域内に、
f(x)が不連続になる点x=xg
が存在する事を意味します。
(最大値の定理の対偶の定理の証明おわり)
(補足)
以上の証明の中で出てきた、
(x≠xgでは)有限の値Mに制限される極限値があっても、
x=xgの場合のf(x)が有限の値Mに制限されない関数とは、
例えば、大学の数学で学ぶ、ディラックのデルタ関数というものがあります。
x≠0のとき: δ(x)=0
x=0のとき: δ(x)=無限大(有限の値Mに制限されない)
そして、
xのー1から1の範囲で定積分すると:
となる関数です。
(最大値の定理の証明のポイント)
以上の、最大値の定理の証明のポイントは、関数f(x)の定義される区間内の関数値f(x)が有限の値Mに制限されない場合を詳しく調べた、定理の対偶の定理を証明した事にあります。
関数値f(x)が有限の値Mに制限されないという事は、
(1)f(x)の値が有限の値Mに制限されない区間がある場合は、f(x)の値が制限されない区間の幅を無限に狭め、その無限に狭めた区間を少なくとも1点に収束させる極限がある事を確認した事。
(2)そして、その収束した極限の点xgでは、関数f(x)が不連続になる事をしらべた事が、最大値の定理の証明のポイントです。
よって、この対偶が成り立ち:
閉区間で連続である関数においては、f(x)が有限の値Mに制限されないという事が無いのです。
(備考1)
なお、下図の様に、少なくとも1つの端(x=a)が開区間で連続な関数については、そのx=aとなる点が無限に発散する点になり得るので、f(x)がx=aの極限で無限に発散する場合があり得ます。
なお、学生が微分積分を無駄なく学べるよう工夫がこらされている本:小平邦彦「[軽装版]解析入門Ⅰ」では、
【閉区間で連続な関数の最大値・最小値の定理】を、閉区間の連続関数は一様連続であり、開区間の関数は一様連続で無いという、関数の本質的な性質を使って証明しています。小平邦彦「[軽装版]解析入門Ⅰ」の85ページにその証明が書いてありますので、是非、一読する事をお勧めします。
小平邦彦「[軽装版]解析入門Ⅰ」で学ぶならば、微分積分が無駄なく勉強できて良いと思います。
(一様連続性と最大値・最小値の定理の関係)
こうして証明できた、閉区間で連続な関数の最大値・最小値の定理によって、
f(x)が連結な閉区間a≦x≦bで1つながりに連続な関数であれば、f(x)の値はある最大値と最小値の間の値に限られている。
その、最大値と最小値の間の値に限られている、閉区間で連続な関数f(x)の領域を以下の図の様に2等分する。
(ただし、二等分とは言っても、分割された領域の境界点は、それぞれの領域が共有するように分割する。)
そして、分割された領域毎に、関数の最大値と最小値の差Δを考え、全分割領域での、差Δの最大値Δ2を抽出する。
関数f(x)が連続関数の場合は、その差の最大値Δ2は、分割前の領域での関数の最大値と最小値の差Δ1よりも小さくなる。
更に、各領域を2等分する。
(ただし、二等分とは言っても、分割された領域の境界点は、それぞれの領域が共有するように分割する。)
そして、分割された領域毎に、関数の最大値と最小値の差Δを考え、全分割領域での、差Δの最大値Δ3を抽出する。
関数f(x)が連続関数の場合は、その差の最大値Δ3は、分割前の領域での差の最大値Δ2よりも小さくなる。
更に、各領域を2等分する操作を繰り返し、
差の最大値Δ4、Δ5、Δ6・・・
を求めて行く。
すると、関数f(x)が連続関数の場合は、領域を分割する毎に、全分割領域での差の最大値Δnは無限に小さくなって行く。
(もし関数の最大値と最小値の差Δnが無限に小さくならない点があったならば、その点は連続では無い点である。連続関数f(x)には、そのような点は無い。)
(一様連続性)
以上の様に、ある関数f(x)の各分割領域を更に2分の1に分割する操作をn回繰り返していき、各分割領域の関数f(x)の最大値と最小値の差(関数の値のばらつき)Δを求める。
(1)そのとき、全ての分割領域での関数の値のばらつきΔの最大値Δnが有限の値で存在すること。
(2)この操作を繰り返して分割領域を無限に小さくすると、
全ての分割領域での関数の値のばらつきの最大値Δnが、無限に小さくなって行く。
(すなわち、全ての分割領域での関数の値のばらつきがΔnより小さく、そのΔnが無限に小さくなっていく)
これが成り立つ関数f(x)の性質を「一様連続」であると言います。
(一様連続の説明おわり)
その様に無限に小さい差Δnは、関数f(x)の値の総和(リーマン積分)への影響が無限に小さいため、この関数f(x)は、リーマン積分が可能です。
【閉区間で連続な関数の最大値・最小値の定理】を、閉区間の連続関数は一様連続であり、開区間の関数は一様連続で無いという性質を使って証明しているのは、一様連続性が、最大値・最小値の定理が成り立つ根本的な原因であるという数学的視点が大事である事を教えたいからではないかと考えます。是非、一読をお勧めします。
リンク: